На бесконечном поле имеется вертикальная стена. Длина стены неизвестна. От нижнего конца стены влево отходит горизонтальная стена также неизвестной длины. Робот находится в клетке, расположенной справа от верхнего края вертикальной стены. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

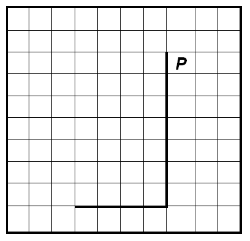
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные правее вертикальной стены, ниже горизонтальной стены и угловую клетку. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

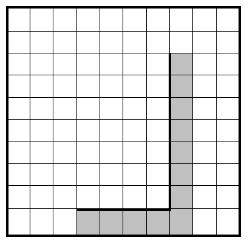
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным.

Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля.

Сохраните алгоритм в формате программы Кумир. Название файла и каталог для сохранения Вам сообщат организаторы.

На бесконечном поле имеется вертикальная стена. Длина стены неизвестна. От верхнего конца стены влево отходит горизонтальная стена также неизвестной длины. Робот находится в клетке, расположенной справа от нижнего края вертикальной стены. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

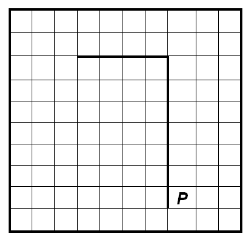
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные правее вертикальной стены, выше горизонтальной стены и угловую клетку. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

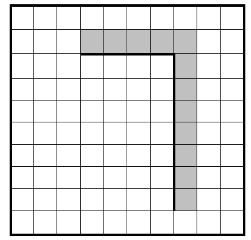
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным.

Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля.

Сохраните алгоритм в формате программы Кумир. Название файла и каталог для сохранения Вам сообщат организаторы.

На бесконечном поле есть две горизонтальных стены. Стены имеют одинаковую длину. Левые концы стен и правые концы стен находятся на одной вертикали (то есть стены находятся точно одна над другой). Расстояние между стенами неизвестно, но не менее одной клетки. Длины стен неизвестны. Робот находится в клетке, расположенной непосредственно над нижней стеной у её левого конца. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

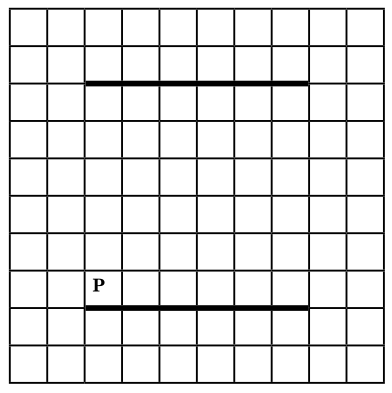
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно выше верхней стены, и клетки, расположенные непосредственно выше нижней стены, кроме клетки, в которой находится Робот перед выполнением программы. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

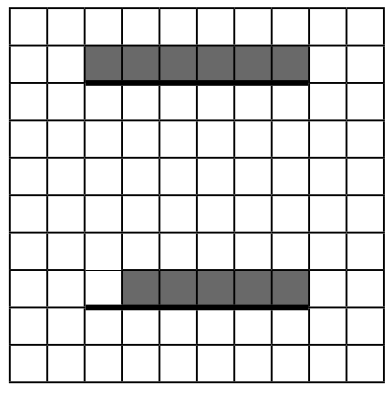
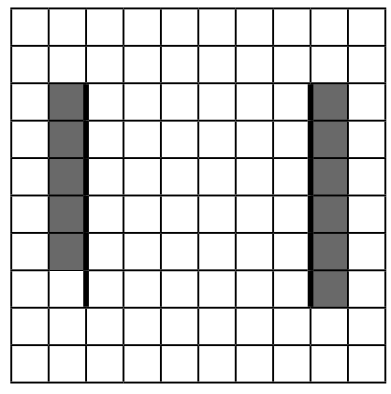
На бесконечном поле есть две вертикальных стены. Стены имеют одинаковую длину. Верхний и нижний концы стен находятся на одинаковой высоте. Расстояние между стенами неизвестно, но не менее одной клетки. Длины стен неизвестны. Робот находится в клетке, расположенной непосредственно слева от левой стены и её нижнего конца. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

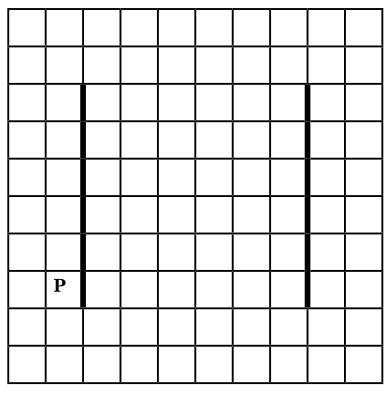
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно правее правой стены, и клетки, расположенные непосредственно левее левой стены, кроме клетки, в которой находится Робот перед выполнением программы. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого расположения стен. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в текстовом файле. Название файла и каталог для сохранения Вам сообщат организаторы экзамена.

На бесконечном поле есть две вертикальных стены одинаковой высоты. Верхние и нижние концы стен находятся на одной высоте. Длины стен неизвестны. Расстояние между стенами неизвестно, но не менее одной клетки. Робот находится в клетке, расположенной непосредственно справа от левой стены у её верхнего конца. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

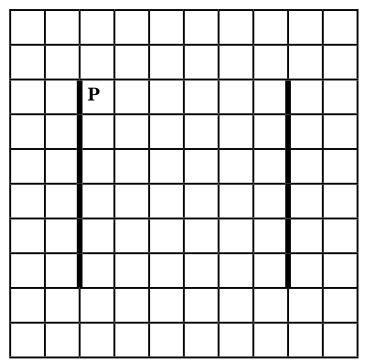
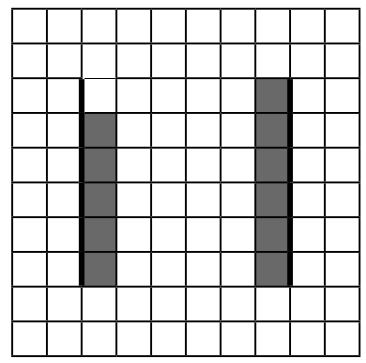
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно левее правой стены, и клетки, расположенные непосредственно правее левой стены, кроме клетки, в которой находится Робот перед выполнением программы. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

На бесконечном поле есть горизонтальная и вертикальная стены. Левый конец горизонтальной стены соединён с верхним концом вертикальной стены. Длины стен неизвестны. Робот находится в клетке, расположенной непосредственно слева от вертикальной стены у её нижнего конца. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

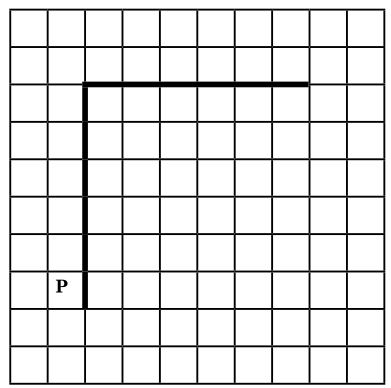
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно выше горизонтальной стены, и клетки, расположенные непосредственно ниже горизонтальной стены. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).