Решение:

При \( x \geqslant 0 \) функция имеет вид \( y = x^2 - 5x \). На этом отрезке её график - часть параболы \( y = x^2 - 5x \) с вершиной \( x_0 = \dfrac{5}{2 } = - 2.5, \) \( y_0 = - 6.25. \) Нули функции на этом отрезке \( 0; \,\, 5 \).

При \( x < 0 \) функция имеет вид \( y = x^2 +3x \). На этом интервале её график - часть параболы \( y = x^2 +3x \) с вершиной \( x_0 = - \dfrac{3}{2 } = -1.5 , \) \( y_0 = - 2.25. \) Нули функции на этом отрезке \( -3; \,\, 0 \).

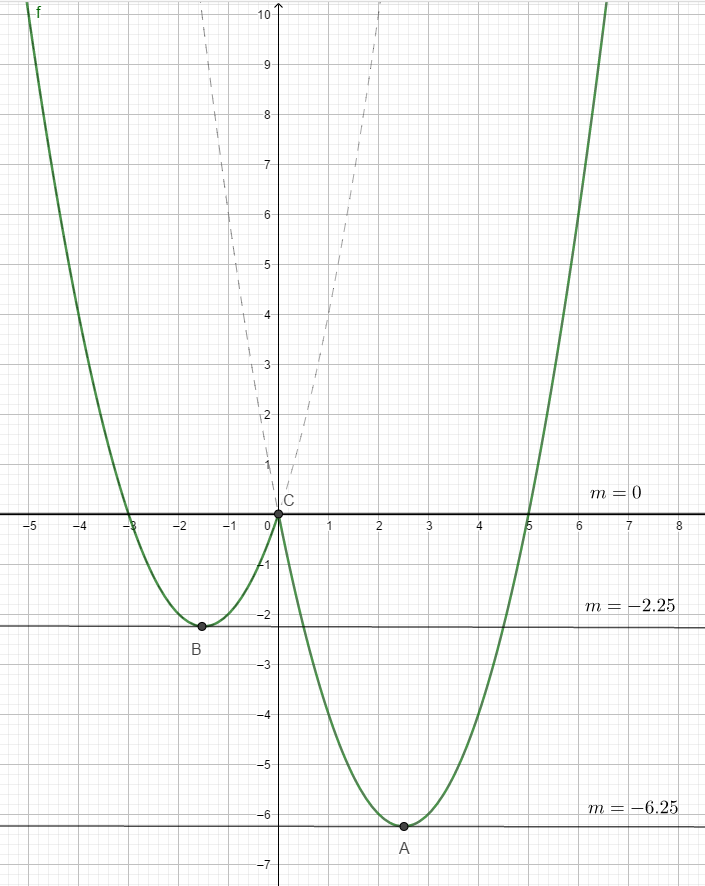
Из графика видно, что при \( m < -6.25 \) прямая \( y = m \) не имеет общих точек с графиком функции \( y = x^2 - 4 |x| - x .\)

При \( m = -6.25 \) прямая \( y = m \) пересекает график функции \( y = x^2 - 4 |x| - x \) в единственной точке \( A (2.5; \,\, -6.25 ) \).

При \( -6.25 < m < -2.25 \) прямая \( y = m \) пересекает график функции \( y = x^2 - 4 |x| - x \) в двух точках.

При \( m = -2.25 \) прямая \( y = m \) имеет с графиком функции \( y = x^2 - 4 |x| - x \) три общие точки.

При \( -2.25 < m < 0 \) прямая \( y = m \) имеет с графиком функции \( y = x^2 - 4 |x| - x \) четыре общие точки.

При \( m = 0 \) прямая \( y = m \) имеет с графиком функции \( y = x^2 - 4 |x| - x \) три общие точки.

При \( m > 0 \) прямая \( y = m \) имеет с графиком функции \( y = x^2 - 4 |x| - x \) две общие точки.

Ответ: \( m \in [ -6.25; \, -2.25 ] \cup [0; \, + \infty ) \)