Решение:

а) При \(x + 2 \geqslant 0,\) т.е. при \(x \geqslant -2\) получаем, что \(y = 3x + 6 - x^2 -3x -2,\) т.е. \(y(x) = -x^2 + 4.\) График такой функции представляет кусок параболы, построенный на полуинтервале \([-2, \, + \infty)\). Ветви этой части параболы направлены вниз. Её вершина находится в точке \((0, \, 4)\). Из условия \(-x^2 + 4 = 0\) находим, что график этой функции пересекает ось абсцисс в точках \((-2, \, 0)\) и \((2, \, 0).\)

При \(x < -2\) получаем, что \(y = -3x - 6 - x^2 -3x -2,\) т.е. \(y = -x^2 -6x -8.\) График этой функции тоже кусок параболы, построенный на интервале \((-\infty; \, -2).\) Ветви тоже направлены вниз. Так как \(x_0 = - \cfrac{-6}{2 \cdot(-1)} = -3,\) \(y_0 = - (-3)^2 -6 \cdot (-3) - 8 = -1,\) то вершина \((-3, \, -1)\) этого куска параболы лежит в нашем интервале. Точки пересечения графика с осью абсцисс легко найти из условия \(-x^2 -6x - 8 = 0,\) или \(x^2 +6x + 8 = 0.\) Откуда по теореме Виета находим, что \(x_1 = -4, \) \(ч_2 = -2.\) .

В точке \((-2, \, 0)\) две части графика «сшиваются». График функции выглядит следующим образом:

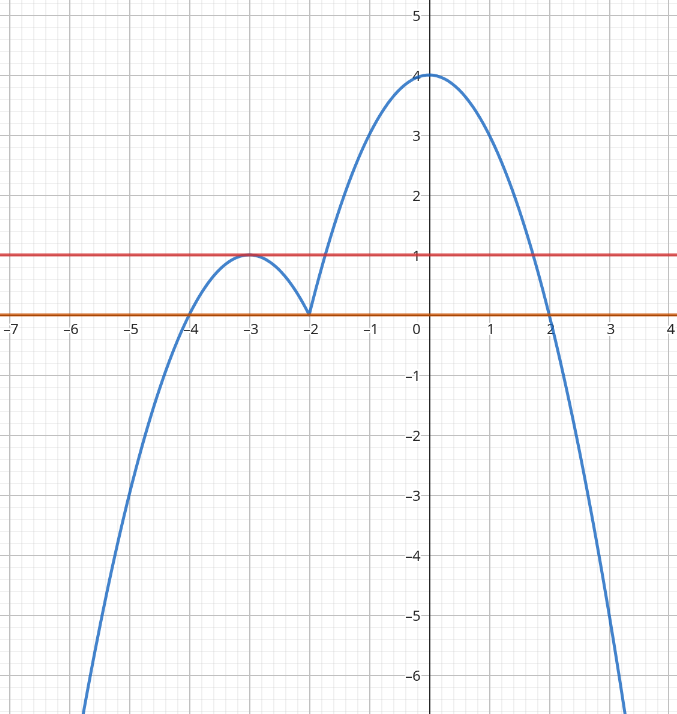
б По графику легко видно, что только две прямые \(y = 0\) и \(y = 1\) пересекают график функции из части а) в трёх точках.

Ответ:б) \(0; \, 1\)