Задание 23. Вариант 1
- Просмотры: 250
- Изменено: 1 февраля 2025
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как \( 6 : 13 : 17 \). Найдите радиус окружности, если меньшая из сторон равна \( 18. \)
Решение:
Длина дуги пропорциональна величине центрального угла, который вырезает её из окружности. Значит, \( 6x + 13x + 17x = 360^\circ \), то есть \( x = 10^\circ \). Наименьшая сторона (обозначим её как \( AB \)), стягивает дугу в \( 60^\circ \). Но, тогда \( \Delta AOB \) - равносторонний, поэтому \( R = OA = AB = 18. \)
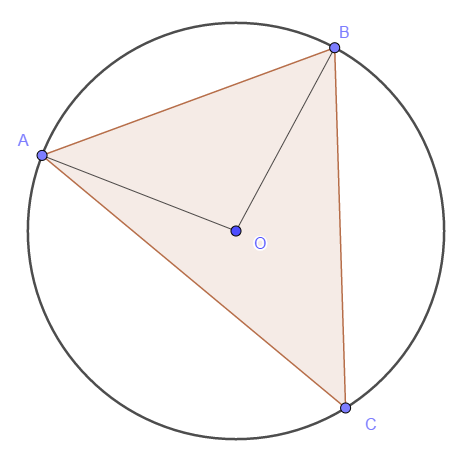
Ответ: \( 18 \).