Задание 23. ОГЭ. Математика. Статград 2024-1
- Просмотры: 76
- Изменено: 23 ноября 2024
Прямая, параллельная основаниям трапеции \(ABCD\) , пересекает её боковые стороны \(AB\) и \(CD\) в точках \(E\) и \(F\) соответственно. Найдите длину отрезка \(EF\) , если \(AD = 33\), \(BC =18\) , \(CF : DF = 2 :1\) .
Решение:
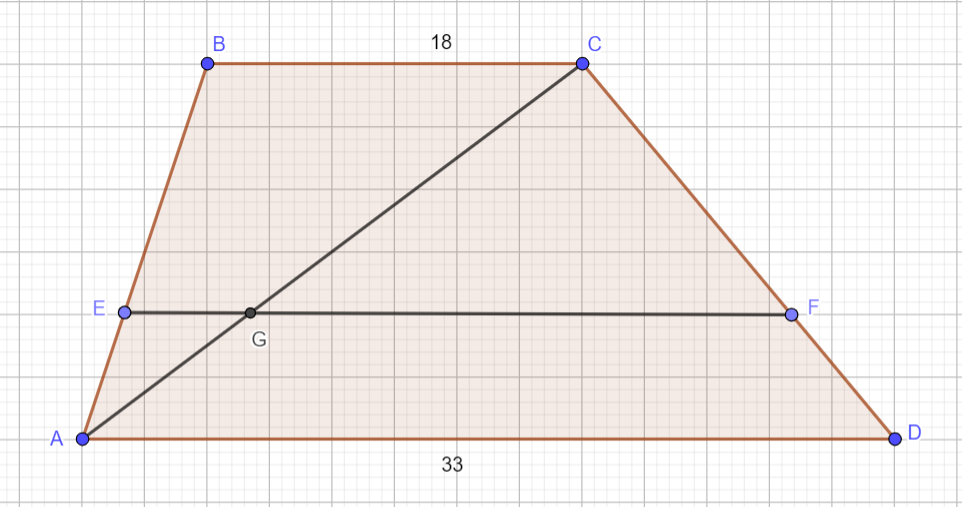
Проведём диагональ \(AC\). Тогда \(\Delta AEG \sim \Delta ABC\) по двум углам (угол \(A\) общий, \(\angle E = \angle B \) как соответственные углы при параллельных прямых \(EG\) и \(BC\)). Поэтому $$ \frac{AE}{AB} = \frac{EG}{BC} \Rightarrow \frac{1}{3} = \frac{EG}{18} \Rightarrow EG = 6. $$ Аналогично, \( \Delta CGF \sim \Delta CAD \). Отсюда $$ \frac{CF}{CD} = \frac{GF}{AD} \Rightarrow \frac{2}{3} = \frac{GF}{33} \Rightarrow GF = 22. $$ Окончательно, \(EF = EG + GF = 6 + 22 = 28\).
Ответ: \( 28 \).