Задание 24. Вариант 1
- Просмотры: 71
- Изменено: 22 ноября 2024
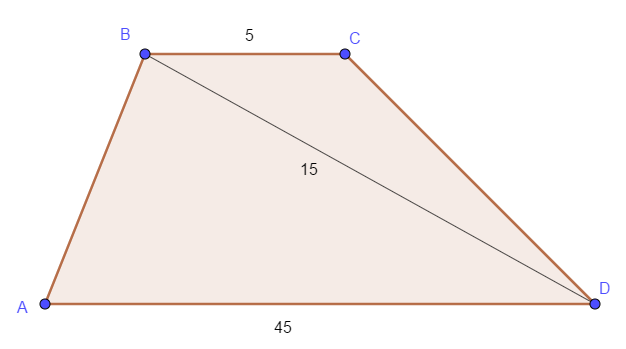
Основания \( BC \) и \( AD \) трапеции \( ABCD \) равны соответственно \( 5 \) и \( 45 \), \( BD = 15 \). Докажите, что треугольники \( CBD \) и \( BDA \) подобны.
Решение:
\( \angle ADB = \angle CBD \) как накрест лежащие углы при параллельных прямых \( AD \) и \( BC \). Кроме того, $$ \frac{AD}{BD} = \frac{BD}{BC} = 3. $$ Поэтому \( \Delta CBD \sim \Delta BDA \) по двум пропорциональным сторонам и углу между ними.
