Задание 24. ОГЭ. Математика. Статград 2024-1-1
- Просмотры: 204
- Изменено: 1 февраля 2025
Сторона \(AD\) параллелограмма \(ABCD\) вдвое больше стороны \(CD\) . Точка \(M\) — середина стороны \(AD\) . Докажите, что \(CM\) — биссектриса угла \(BCD\).
Решение:
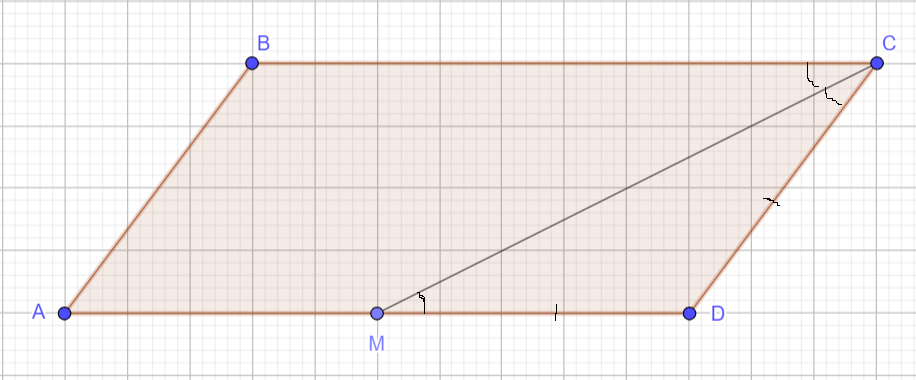
Т.к. \(AD = 2 CD\) и \(M\) — середина \(AD\), то \(MD=CD\). Значит \(\Delta MCD\) — равнобедренный, поэтому \(\angle CMD = \angle MCD\). С другой стороны, \(\angle CMD = \angle MCB\), как накрест лежащие углы при параллельных прямых \(AD\) и \(BC\). Поэтому \(\angle DMC = \angle MCB\), т.е. \(CM\) — биссектриса угла \(BCD\) ч.т.д.