Решение:

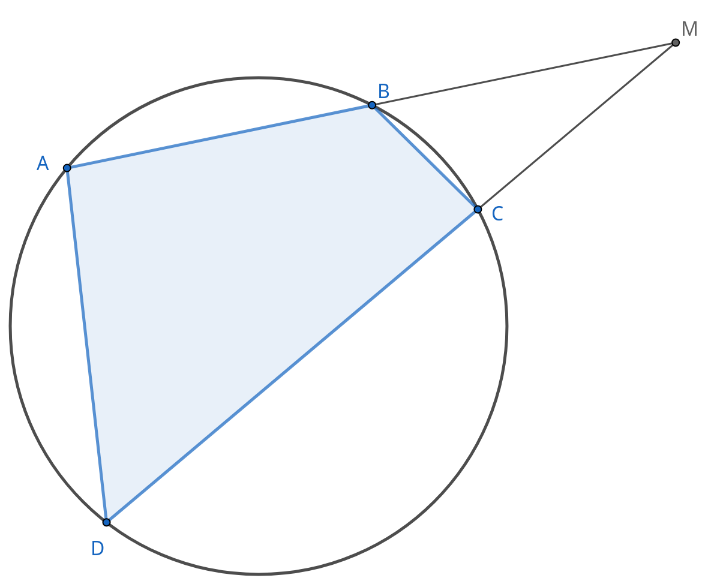
Сумма углов любого четырёхугольника равна \(360^\circ .\) С другой стороны, так как около четырёхугольника \(ABCD\) можно описать окружность, что \(\angle A + \angle C = \angle B + \angle D = 180^\circ .\) В треугольнике \(MBC\) и \(MDA\) угол \(M\) общий. С другой стороны, \(\angle MBC\) и \(\angle CBA\) смежные. Значит \(\angle MBC = 180^\circ - \angle CBA.\) Но по доказанному выше \(\angle ADC = 180^\circ - \angle CBA.\) Значит треугольники \(MBC\) и \(MDA\) подобны по двум углам.