Решение:

Способ 1

\( BM \) - медиана, поэтому \( S_{ABM} = S_{CBM} .\)

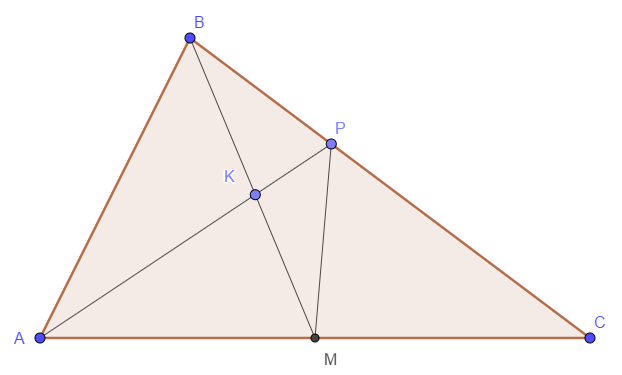
Далее, \( BK : KM = 6 : 7 \), тогда если \( S_{ABK} = 6y \), то \( S_{AMK} = 7y \) и \( S_{ABM} = 13 y \), \( S_{ABC} = 26 y \). Пусть \( S_{BPK} = x\), тогда \( S_{PMK} = \dfrac{7}{6} x \). Наконец, \( S_{APM} = S_{CPM} \). Отсюда получаем $$ S_{APC} = 26y - (6y + x) = 2 (7y + \frac{7}{6} x) $$ $$ 20 y - x = 14 y + \frac{7}{3} x \quad \Rightarrow \quad x= \frac{9}{5} y $$

Окончательно $$ \frac{S_{BPK}}{S_{ABK}} = \frac{x}{6y} = \frac{3}{10} $$

Способ 2

\( BM \) - медиана, поэтому \( S_{ABM} = S_{CBM} .\) Пусть \( S_{ABM} = S \).

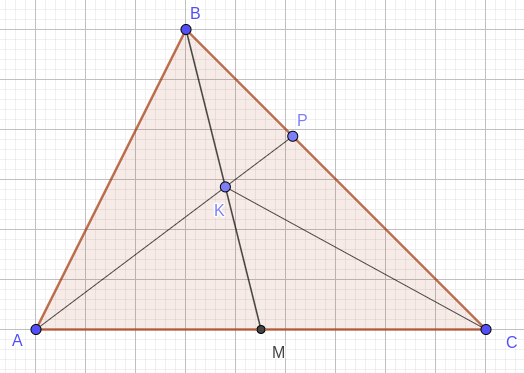
Тогда \( S_{ABK} = \dfrac{6}{13} S, S_{AKM} = \dfrac{7}{13} S.\) Так \( KM \) - медиана в треугольнике \( AKM \), то \( S_{CKM} = S_{AKM} = \dfrac{7}{13}S \) и, значит, \( S_{AKC} = \dfrac{14}{13}S, S_{BKC} = \dfrac{6}{13}S \).

Пусть \( S_{BKP} = X \), тогда \( S_{PKC} = \dfrac{6}{13}S - X \). Теперь $$ \frac{S_{ABK}}{S_{BKP}} = \frac{S_{AKC}}{S_{PKC}}, \quad \Rightarrow \frac{3}{X} = \frac{7}{\cfrac{6}{13}S - X}. $$ Отсюда \( X = \dfrac{9}{5 \cdot 13} S \). Окончательно, $$ \frac{S_{BPK}}{S_{ABK}} = \frac{9}{5 \cdot 13} : \frac{6}{13} = \frac{3}{10}. $$

Ответ: \( 3 : 10 \).