Решение:

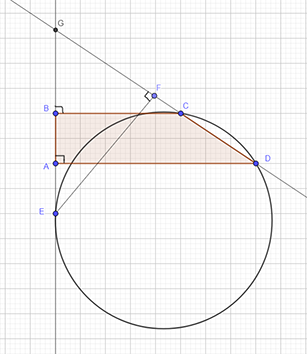
Пусть прямые \(AB\) и \(CD\) пересекаются в точке \(G\). Опустим перпендикуляр \(EF\) на \(CD\). Треугольники \(AGD\) и \(BGC\) подобны (они являются прямоугольными треугольниками и у них общий угол \(G\) ). Пусть \(GC = x\). Тогда $$ \frac{GC}{BC} = \frac{GD}{AD} \Rightarrow \frac{x}{12} = \frac{GD}{14} \Rightarrow GD = \frac{7x}{6}. $$ По теореме о касательной и секущей \(GE^2 = GC \cdot GD\). Отсюда $$ GE = \sqrt{\frac{7}{6}} x $$ Из треугольника \(GBC\) находим, что $$ \sin G = \frac{BC}{GC} = \frac{12}{x}. $$ Теперь, $$ EF = GE \sin G = \sqrt{\frac{7}{6}} x \cdot \frac{12}{x} = 2 \sqrt{42}. $$

Ответ: \( 2 \sqrt{42} \).