Решение:

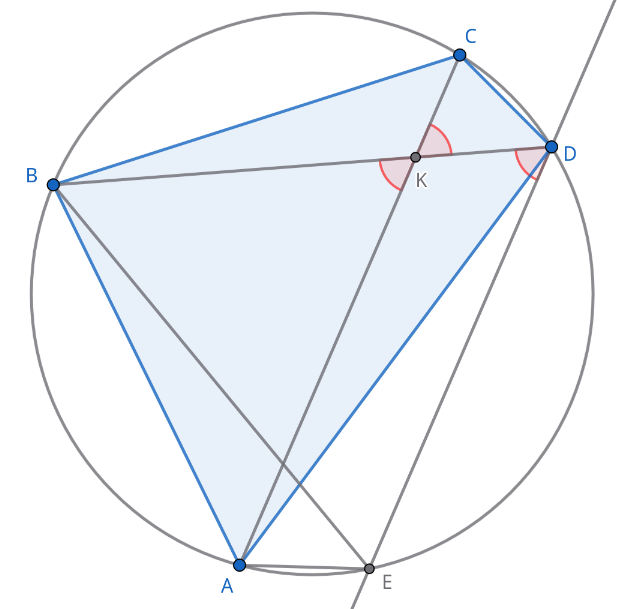
Проведём через точку \(B\) прямую, параллельную диагонали \(AC\) и пусть она пересекает окружность в точке \(E.\) Получившаяся трапеция \(ACDE\) вписана в окружность. Значит она равнобедренная и \(AE = CD = 8.\) Далее \(\angle AKB = \angle CKD = 60^\circ\) как вертикальные, \(\angle EDB = \angle CKD = 60^\circ\) как накрест лежащие при параллельных прямых \(AC\) и \(DE.\) Четырёхугольник \(ABDE\) вписан в окружность, значит \(\angle BAE + \angle BDE = 180^\circ ,\) отсюда \(\angle BAE = 180^\circ - 60^\circ = 120^\circ .\) По теореме косинусов $$BE^2 = AB^2 + AE^2 - 2 AB \cdot AE \cdot \cos 120^\circ = 44^2 + 8^2 + 44 \cdot 8 = 2352.$$ Значит, \(BE = \sqrt{2352}.\) По теореме синусов теперь находим, что $$R = \frac{BE}{2 \sin 120^\circ} = \frac{\sqrt{2352}}{\sqrt{3}} = \sqrt{\frac{2352}{3}} = \sqrt{784} = 28.$$

Ответ: \(28\)