Решение:

а) Угол между скрещивающимися прямыми \(MP\) и \(AB\) равен углу между пересекающимися прямыми \(MP\) и \( A_1B_1\). Т.к. треугольник \( A_1B_1C_1 \) равнобедренный, то \( B_1M \bot A_1C_1 \). По теореме о трёх перпендикулярах \( A_1 C_1 \bot MP \).

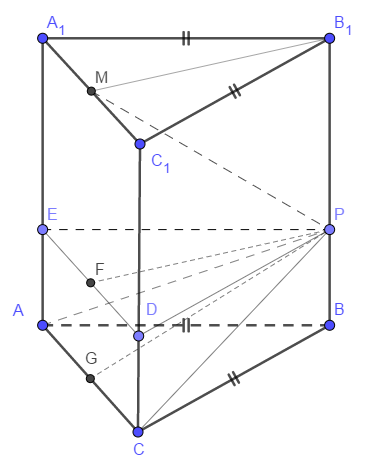
б) Проведём через точку \( P \) плоскость \( (EDP) \), параллельную \( (A_1 B_1 C_1) \). Угол между \( (A_1 B_1 C_1) \) и \( (ACP)\) равен углу между \( (EDP)\) и \( (ACP)\). Плоскость \( (ACP) \) пересекает параллельные плоскости \( (EDP)\) и \( (ABC)\) по параллельным прямым: \(AC\) и пралаллельной ей прямой \(m\), проходящей через точку \( P \). Перепендикуляры к точке \(P\) в плоскостях \( (EDP) \) и \( (ACP)\) тогда будут перпендикулярами к параллельным к \(m\) прямым \( ED \) и \(AC\). Перпендикуляр \( PF \) к \( ED\) — это высота равнобедренного треугольника \( EDP \), проведённая к основанию \( ED =32 \). Боковые стороны этого треугольника \( EP =DP = 20 \). По теореме Пифагора \( PF = 12 \).

Пусть \( G\) — середина \( AC \). Тогда \( PG \bot AC \) по соображениям, аналогичным пункта а). Поэтому \( FG = BP = \dfrac{1}{4} BB_1 = 6 \). Окончательно, \( \tan \angle FPG = \dfrac{1}{2} \).

Ответ: б) \( \dfrac{1}{2} \).