Задание 14. Вариант 2
- Просмотры: 964
- Изменено: 1 февраля 2025
В правильной шестиугольной пирамиде \( SABCDEF \) с вершиной \( S \) боковое ребро вдвое больше стороны основания.
а) Докажите, что плоскость, проходящая через середину рёбер \( SA \) и \( SE \) и вершину \( C \), делит ребро \( SB \) в отношении \( 1 : 3 \), считая от вершины \( B \).
б) Найдите отношение, в котором плоскость, проходящая через середины рёбер \( SA \) и \( SE \) и вершину \( C \), делит ребро \( SF \), считая от вершины \( S \).
Решение:
а) Пусть \(H\) — середина ребра \(SA\), \(G\) — середина ребра \(SE\). Тогда \(HG\) — средняя линия треугольника \(SAE\), и, значит, прямая \(HG\) параллельна плоскости основания пирамиды.
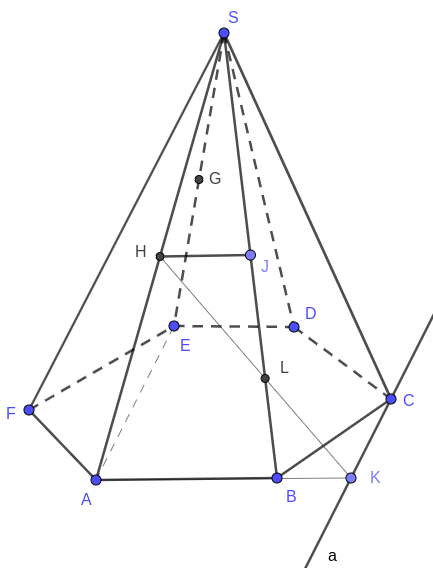
Плоскость сечения \( (HGC)\) будет пересекать плоскость основания пирамиды по прямой \(a\), параллельной \(HG\) и проходящей через точку \(C\).
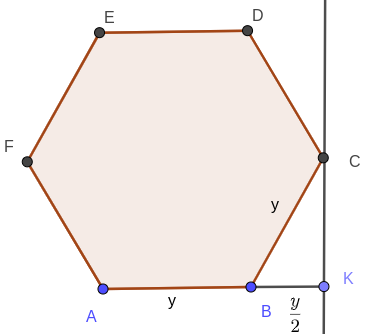
Продлим отрезок \( AB\) до пересечения с прямой \(a\). Точка \(K \in a\), с другой стороны она лежит в плоскости грани \( SAB\). Значит, прямая \(HK\) лежит в плоскости сечения \((HGC)\). Точка \(L = HK \cap SB\) — точка, по которой плоскость сечения пересекает ребро \(SB\). Докажем, что \(BL : LS = 1:3\). Треугольник \(CBK\) — прямоугольный, \(\angle BCK = 30^\circ\). Если сторона шестиугольника \(ABCDEF\) равна \(y\), то катет \(BK = \dfrac{y}{2}\). Проведём через точку \(H\) параллельно \(AB\) отрезок \(HJ\) в плоскости грани \(SAB\). Тогда \(HJ\) — средняя линия треугольника \(SAB\), причём \( HJ = \dfrac{y}{2}\). Так как \( HJ \parallel BK\), то \( \angle HJL = \angle LKB\), \( \angle JHL = \angle LBK\), значит \(\Delta HJL = \Delta KBL\), поэтому $$LB = LJ = \frac{JB}{2} = \frac{SB}{4}.$$ А это и означает, что \(LB : LS = 1:3\).
б) Чтобы найти точку пересечения плоскости сечения \(HGC\) с ребром \(SF\) продлим отрезок \( FA\) до пересечения с прямой \(a\).
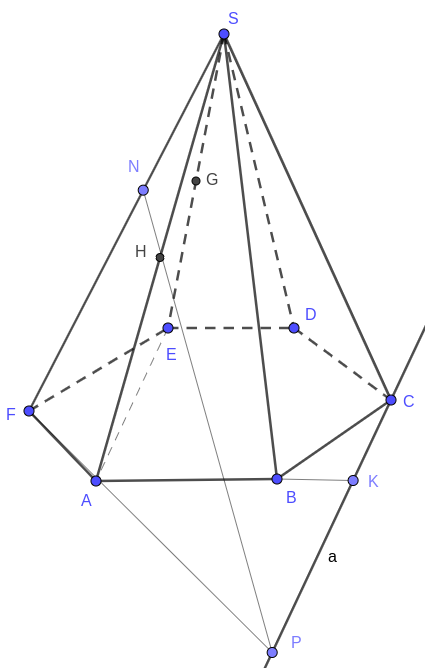
Пусть \(P\) — точка их пересечения. Прямая \(HP\) — это прямая, по которой плоскость сечения \( (HGC)\) пересекает плоскость грани \(SFA\). Пусть \(N\) — точка пересечения прямых \(HP\) и \(SF\).
Треугольник \(AKP\) — прямоугольный, причём \(\angle APK = 30^\circ\). Так как \(AK = \dfrac{3y}{2}\), то \(AP = 3y.\)
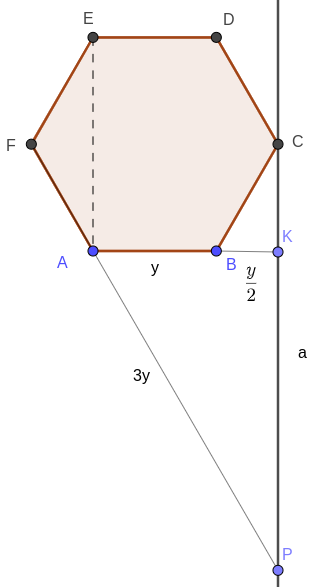
Проведём в равнобедренном треугольнике \(SAF\) среднюю линию \(HQ\) параллельно стороне \(SF\). Если \(SF = 2x\), то \(HS = HA = x\). Далее, так как \(HQ \parallel NF\), то треугольники \(PHQ\) и \(PNF\) подобны. Это означает, что $$ \frac{HQ}{NF} = \frac{PQ}{PF}. $$
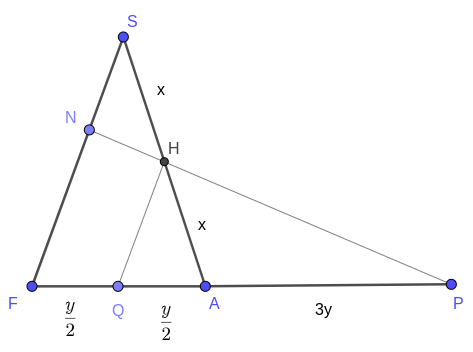
Отсюда $$ NF = \frac{PF \cdot HQ}{PQ} = \frac{4y \cdot x \cdot 2}{7y} = \frac{8x}{7} $$ $$ SN = 2x - \frac{8x}{7} = \frac{6x}{7} $$ Окончательно, $$ \frac{SN}{NF} = \frac{3}{4} $$
Ответ: б) \(3:4\).