Решение:

а) Точка \( O \) лежит на высоте \( AM \) равностороннего треугольника \( ABC \), причём \( AO : OM = 2 : 1 \). Апофема \( SM \) перпендикулярна \( BC \). Кроме того, \( SM = AM = 6 \sin 60^\circ = 3 \sqrt{3} \).

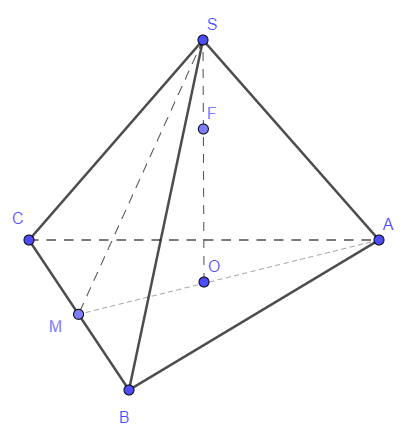
Плоскость \( (CMF) \) пересекает плоскость \( (SMA) \) по прямой \( MF \). Продлим эту прямую до пересечения с \( SA \) в точке \( G \). В этой точке плоскость \( (CMF) \) пересекает отрезок \(SA\).

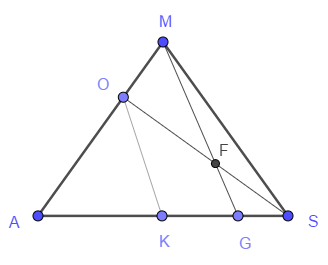
Проведём в треугольнике \( SMA \) через точку \( O\) прямую, параллельную \( MG \). Пусть она пересечёт \( SA \) в точке \( K \). По теореме Фалеса с одной стороны \( SG : GK = SF : FO = 1 : 2 \). С другой стороны, \( GK : KA = MO : OA = 1 : 2 \). Поэтому, если \( SG = x \), то \( GK = 2x \), \( KA = 4x \). Отсюда, \( SG : GA = 1 : 6 \).

б) \( (MCF) \cap (ABC) = BC \). Так как \( AM \bot BC \), то по теореме о трёх перпендикулярах \( FM \bot BC \). Отсюда угол между плоскостями \( (MCF) \) и \( (ABC) \) — это угол между прямыми \( MF \) и \( MO \). Итак, \( MO = \dfrac{1}{3} MA = \sqrt{3} \). По теореме Пифагора $$ SO = \sqrt{SM^2 - MO^2} = \sqrt{27 - 3} = 2 \sqrt{6}. $$ $$ FO = \frac{2}{3} SO = \frac{4 \sqrt{6}}{3}. $$ $$ \tan \angle FMO = \frac{FO}{MO} = \frac{4 \sqrt{6}}{3} : \sqrt{3}= \frac{4 \sqrt{2}}{3}. $$ Отсюда \( \angle FMO = \arctan \dfrac{4 \sqrt{2}}{3} \).

Ответ: а) \( 1:6 \); б) \( \arctan \dfrac{4 \sqrt{2}}{3} \).