Решение:

а) Пусть \( O \) — точка пересечения диагоналей квадрата \( ABCD \). Тогда \( BO = DO \). Так как равнобедренные треугольники \( BSC \) и \( DSC \) равны, то \( LB = LD \). Поэтому медиана \( LO \), проведённая к основанию \( BD \) является и высотой. Значит \( BO \bot LO \).

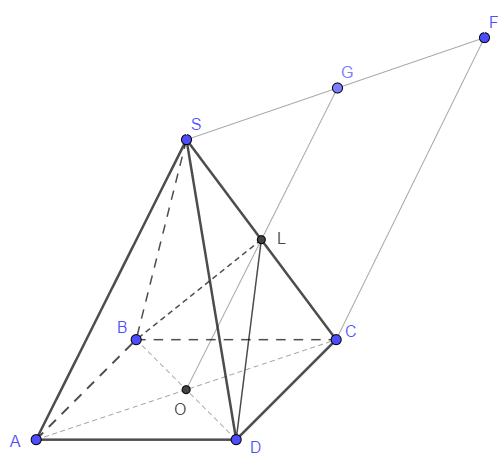
б) Достроим треугольник \( ASC \) до параллелограмма \( ASFC \) (\( AS \parallel CF, \, AC \parallel SF \) ). Пусть \( G \) — середина \( SF \). Тогда \( GO = AS = 2 LO \). $$ LO = \frac{BO}{\tan \angle BLO} = 2 \sqrt{5}, \quad \Rightarrow \quad AS = 4 \sqrt{5}. $$

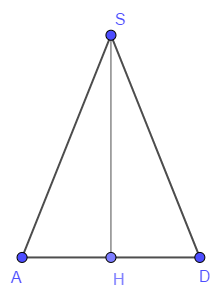
Теперь \( SH = \sqrt{SA^2 - AH^2} = \sqrt{4^2 \cdot 5 - 4^2} = 8 \), \( S_{ASD} = \dfrac{1}{2} AD \cdot SH = 32\). Полная поверхность пирамиды $$ S_{SABCD} = 4 S_{ASD} + S_{ABCD} = 4 \cdot 32 + 64 = 192. $$

Ответ: б) \( 192 \).