Задание 14. Вариант 5
- Просмотры: 157
- Изменено: 1 февраля 2025
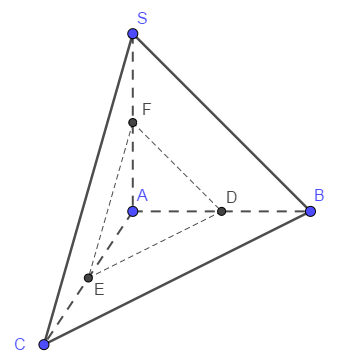
Ребро \( SA \) пирамиды \( SABC \) перпендикулярно плоскости основания \( ABC .\)
а) Докажите, что плоскость, проходящая через середины рёбер \( AB \), \( AC \) и \( SA \), отсекает от пирамиды \( SABC \) пирамиду, объём которой в \( 8 \) раз меньше объёма пирамиды \( SABC. \)
б) Найдите расстояние от вершины \( A \) до этой плоскости, если \( SA = 2 \sqrt{5} \), \( AB = AC = 10, \) \( BC = 4 \sqrt{5}. \)
Решение:
а) \( ED \) — средняя линия треугольника \( ABC \). Поэтому \( S_{AED} = \dfrac{1}{4} S_{ABC} \). Кроме того, так как \( FA = \dfrac{1}{2} SA \), то \( V_{SABC} = \dfrac{1}{8} V_{FAED} \).
б) Пусть \(h\) — длина пепендикуляра, опущенного из вершины \( A \) на плоскость \( FED \). Это и будет расстояние от \( A \) до этой плоскости. Для его нахождения воспользуемся методом объёмов. С одной стороны, \( V_{FAED} = \dfrac{1}{3} FA \cdot S_{AED} \). С другой стороны, \( F_{FAED} = \dfrac{1}{3} h \cdot S_{FED} \). Поэтому $$ h = \frac{FA \cdot S_{AED}}{S_{FED}} $$
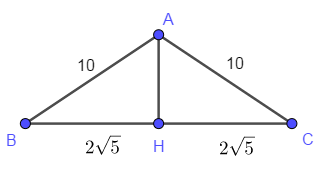
Пусть \( AH \) — высота треугольника \( ABC \). Тогда \( AH = \sqrt{AB^2 - BH^2} = 4 \sqrt{5} \). Его площадь \( S_{ABC} = \dfrac{1}{2} 4 \sqrt{5} \cdot 4 \sqrt{5} = 40\). И \( S_{AED} = 10 \).
Теперь, \( SC = \sqrt{AS^2 + AC^2} = 2 \sqrt{30} \), \( FE = FD = \sqrt{30} \), \( ED = 2 \sqrt{5} \). Высота равнобедренного треугольника \( FED \), опущенная из вершины \( F \) на основание \( ED \) равна \( \sqrt{30 - 5} = 5 \). Поэтому \( S_{FED} = \dfrac{1}{2} 5 \cdot 2 \sqrt{5} = 5 \sqrt{5} \). Окончательно, $$ h = \frac{\sqrt{5} \cdot 10}{5 \sqrt{5}} = 2. $$
Ответ: б) \( 2 \).