Решение:

а) Пусть \( D \) — середина \( AC \), \( E \) — середина \( BC_1 \), \( F \) — середина \( BC \). Тогда \( DF \) — средняя линия треугольника \( ABC \), значит \( DF \parallel AB \). Далее, \( EF \) — средняя линия треугольника \( BB_1 C \), значит \( EF \parallel BB_1 \). Отсюда получаем, что плоскости \( ( AB_1 B )\) и \( (EDF) \) параллельны, поэтому прямые \( AB_1 \) и \( DE \) не пересекаются.

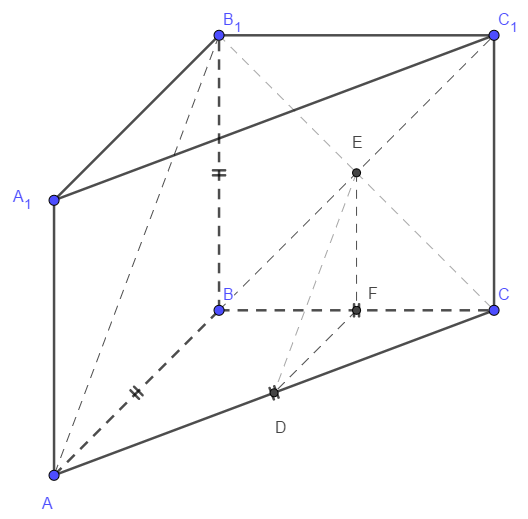
Рассмотрим плоскость \( AB_1E\). Так как \( E \) — точка пересечения диагоналей \(BC_1 \) и \(B_1 C \), то \( C \in (AB_1 E) \), отсюда \( AC \subset (AB_1 E ) \), поэтому \( D \in (AB_1 E) \), и, значит, прямые \( AB_1 \) и \( DE \) лежат в одной плоскости, следовательно они параллельны.

б)Угол между скрещивающимися прямыми \( AB_1 \) и \( BC_1 \) равен углу между пересекающимися прямыми \( BC_1 \) и \( DE \). Так как \( BC = CC_1 = 1 \), то \( BC_1 = \sqrt{2} \), \( BE = \dfrac{\sqrt{2}}{2} \). Так как \( BD \) — высота треугольника \( ABC \), то \( BD = 1 \cdot \sin 60^\circ = \dfrac{\sqrt{3}}{2} \). Наконец, \( FE = FD = \dfrac{1}{2} \), поэтому \( ED = \dfrac{\sqrt{2}}{2} \). Из теоремы косинусов получаем, что $$ \cos \angle BED = \frac{BE^2 + ED^2 - BD^2}{2 \cdot BE \cdot ED}. $$ Подставляя сюда значения сторон треугольника \( EDF \), находим, что \( \cos \angle BED = \dfrac{1}{4} \).

Ответ: б) \( \dfrac{1}{4} \).