Решение:

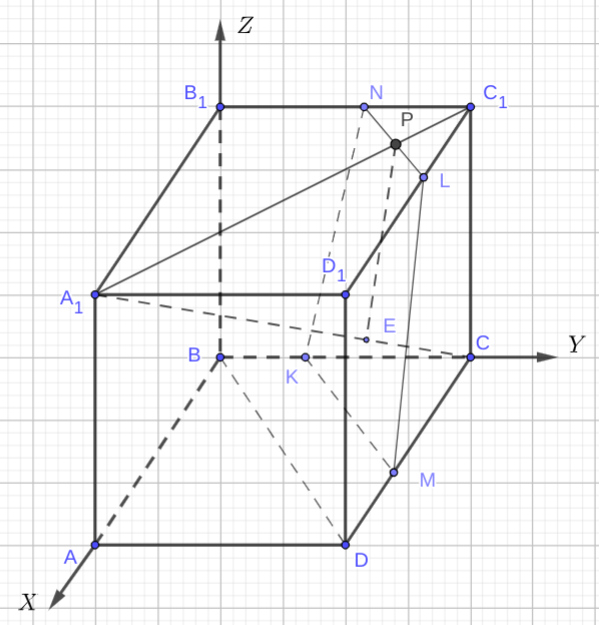
а) Плоскость \(\gamma\) должна пересекать плоскость \(ABC\) по прямой, параллельной \(BD.\) Пусть \(\gamma \cap CD = M.\) Тогда \(CK = CM = 3.\) Аналогично, пусть \(\gamma \cap C_1B_1 = N.\) Тогда \(NL \parallel KM\) и \(C_1L = C_1N = 2.\) Чтобы доказать, что \(A_1C \perp \gamma ,\) докажем, что \(\overrightarrow{A_1C} \perp \overrightarrow{ML}\) и \(\overrightarrow{A_1C} \perp \overrightarrow{MK}.\) Поместим начало координат в точку \(B\). Направляем ось абсцисс вдоль \(AB,\) ось ординат вдоль \(BC,\) ось аппликат вдоль \(BB_1.\) Находим координаты точек: \(A_1 \, (5,~0,~\sqrt{5}),\) \(C \, (0,~5,~0),\) \(K \, (0,~2,~0),\) \(N \, (0,~3,~\sqrt{5}),\) \(M \, (3,~5,~0),\) \(L \, (2,~5,~\sqrt{5}).\) Отсюда получаем координаты векторов: \(\overrightarrow{A_1C} \{-5,~5~,-\sqrt{5}\},\) \(\overrightarrow{ML} \{-1,~0,~\sqrt{5}),\) \(\overrightarrow{MK} \{-3,~-3,~0\}.\) Значит $$\overrightarrow{A_1C} \cdot \overrightarrow{ML} = (-5) \cdot (-1) + 5 \cdot 0 + (-\sqrt{5}) \cdot \sqrt{5} = 0,$$ $$\overrightarrow{A_1C} \cdot \overrightarrow{MK} = (-5) \cdot (-3) + 5 \cdot (-3) + (-\sqrt{5}) \cdot 0 = 0.$$ Это доказывает перпендикулярность прямой \(A_1C\) и плоскости \(\gamma .\)

б) Длина вектора \(\overrightarrow{ML}\) равна \(\sqrt{(-1)^2 + (\sqrt{5})^2} = \sqrt{6}.\) Длина вектора \(\overrightarrow{NK} \, \{ 0,~-1,~-\sqrt{5}\}\) равна тоже \(\sqrt{6}.\) Значит трапеция \(MKNL\) — равнобедренная с основаниями \(NL = 2\sqrt{2}\) и \(MK = 3 \sqrt{2}.\)

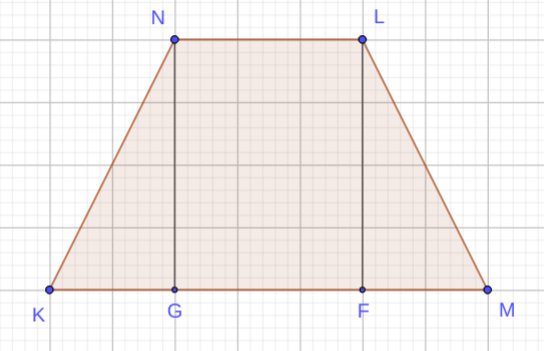
Тогда \(GF = NL = 2 \sqrt{2},\) где \(NG\) и \(LF\) — перпендикуляры, опущенные из вершин \(N\) и \(L\) на основание \(KM.\) Отсюда \(KG = FM = \cfrac{\sqrt{2}}{2}.\) И по теореме Пифагора высота \(LF\) трапеции \(MKNL\) равна \(\sqrt{6 - \cfrac{1}{2}} = \sqrt{\cfrac{11}{2}},\) а её площадь $$ S_{MKNL} = \frac{1}{2} \cdot \frac{2 \sqrt{2} + 3 \sqrt{2}}{2} \cdot \frac{\sqrt{11}}{\sqrt{2}} = \frac{5 \sqrt{11}}{4}.$$ Диагональ \(A_1C = \sqrt{5^2 + 5^2 + (\sqrt{5})^2} = \sqrt{55}.\) Прямоугольный треугольник \(LNC_1\) равнобедренный, причём \(C_1L = C_1N = 2.\) Отсюда \(C_1P = \sqrt{2},\) где \(A_1C_1 \cap NL = P.\) А так как \(A_1C_1 = 5 \sqrt{2},\) то \(A_1P = 4\sqrt{2}.\) Пусть \(A_1C \cap \gamma = E.\) Тогда \(\Delta A_1EP \sim \Delta A_1C_1C\) (они прямоугольные и у них общий угол \(A_1\)). Значит $$\frac{A_1E}{A_1C_1} = \frac{A_1P}{A_1C} \Rightarrow A_1E = \frac{A_1P \cdot A_1C_1}{A_1C}$$ $$A_1 E = \frac{4 \sqrt{2} \cdot 5 \sqrt{2}}{\sqrt{55}} = \frac{8 \sqrt{5}}{\sqrt{11}}.$$ Поэтому, объём пирамиды \(A_1MKNL\) равен $$ V_{A_1MKNL} = \frac{1}{3} \cdot \frac{5 \sqrt{11}}{4} \cdot \frac{8 \sqrt{5}}{\sqrt{11}} = \frac{10 \sqrt{5}}{3} $$

Ответ: б) \(\cfrac{10 \sqrt{5}}{3}\)