Решение:

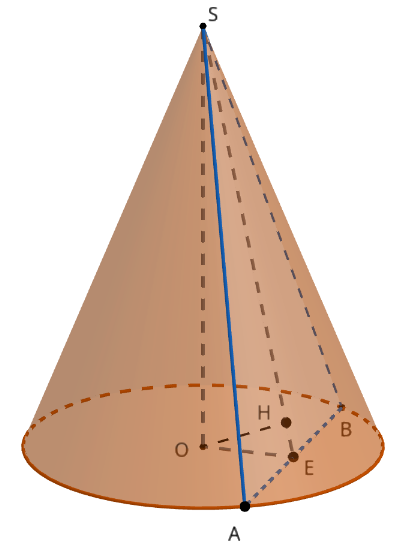
а) Фигурой, получающейся при сечении плоскостью \(SAB\) конуса из условия задачи, является равнобедренный треугольник \(SAB.\) Отметим на основании \(AB\) середину \(E.\) Тогда \(SE \perp AB.\) С другой стороны, в плоскости основания конуса лежит равнобедренный прямоугольный треугольник \(OAB.\) Для него \(OE \perp AB.\) Т.о. угол между плоскостью сечения \(SAB\) и плоскостью основания конуса — это угол \(SEO\) в прямоугольном треугольнике \(SOE.\) Так как \(\triangle OAB\) равнобедренный и прямоугольный, то \(OE = \cfrac{1}{2} AB = 4.\) Значит $$\tan \angle SEO = \frac{SO}{OE} = \cfrac{4 \sqrt{3}}{4} = \sqrt{3} \, \Rightarrow \, \angle SEO = 60^\circ .$$

б) Расстояние от центра основания конуса \(O\) до плоскости \(SAB\) — это высота \(OH,\) опущенная на гипотенузу \(SE\) прямоугольного треугольника \(SEO.\) По теореме Пифагора \(SE = \sqrt{(4 \sqrt{3})^2 + 4^2} = 8.\) Поэтому $$OH = \frac{SO \cdot EO}{SE} = \frac{4 \sqrt{3} \cdot 4}{8} = 2 \sqrt{3}.$$

Ответ: \(2 \sqrt{3}\)