Математика. ЕГЭ. Задание 17. Вариант 1

Математика. ЕГЭ

Задание 17. Вариант 1

Просмотры: 254

Изменено: 1 февраля 2025

На катетах $ AC $ и $ BC $ прямоугольного треугольника $ ABC $ вне треугольника построены квадраты $ ACDE $ и $ BFKC $. Точка $ M $ - середина гипотенузы $ AB $, $ H $ - точка пересечения прямых $ CM $ и $ DK $.

а) Докажите, что прямые $ CM $ и $ DK $ перпендикулярны.

б) Найдите $ MH $, если известно, что катеты треугольника $ ABC $ равны $ 60 $ и $ 80 $.

Решение:

а) Прямоугольные треугольники $ ACB $ и $ DCK $ равны по двум катетам. Поэтому, если $ \angle ABC = \alpha , $ то $ \angle DKC = \alpha $, $ \angle KDC = 90^\circ - \alpha$.

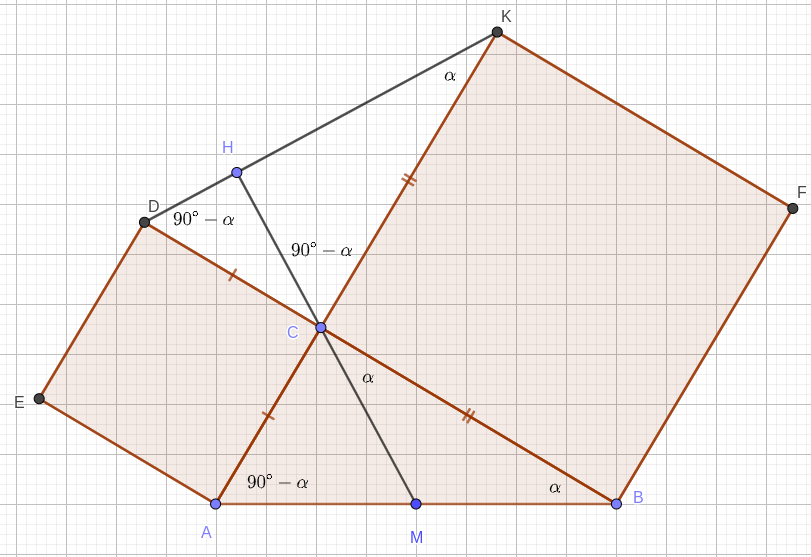
$ CM $ равна половине гипотенузы, т.е. $ MC = MB $. Значит, треугольник $ MCB $ - равнобедренный, поэтому $ \angle MCB = \alpha$ и $\angle HCD = \angle MCB = \alpha$ как вертикальные. Отсюда $\angle HCK = 90^\circ - \alpha$ и $\angle CHK = 180^\circ - (\alpha + 90^\circ - \alpha) = 90^\circ .$

б) Если $AC = 60$ и $BC = 80$, то по теореме Пифагора $AB = \sqrt{60^2 + 80^2} = 100$. Поэтому, $CM = 50$.

$\Delta KCD \sim \Delta KHC$. Отсюда $$ \frac{HC}{CD} = \frac{KC}{KD} \quad \Rightarrow \quad HC = \frac{KC \cdot CD}{KD} = \frac{80 \cdot 60}{100} = 48. $$ Окончательно, $MH = 50 + 48 = 98$.

Ответ: б) $98$.