Решение:

а) \(\angle DCA = \angle KCB = 90^\circ\). Если \(\angle ACB = \alpha\), то \(\angle DCK = 180^\circ - \alpha\).

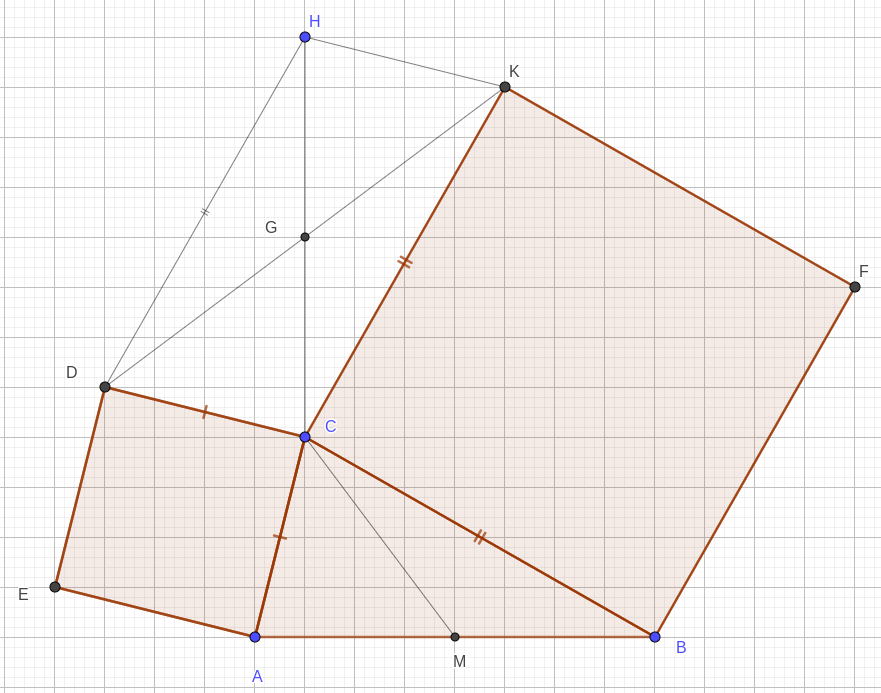
Пусть \(G\) - середина \(DK\). Продлим медиану \(CG\) до точки \(H\) так, что \(CG= GH\). Тогда \(DCKH\) - параллелограмм и, значит, \(\angle HDC = \alpha\). Далее, \(CD = CA\), \(CK = CB\). Поэтому \(\Delta ACB = \Delta CDH\) по двум сторонам и углу между ними. И значит у них равны медианы, проведённые к равным сторонам: $$ CM = DG = \frac{1}{2} DK. $$

б) Пусть \(O\) - центр квадрата \(BFKC\). Тогда \(MO\) - средняя линия треугольника \(ABK\).

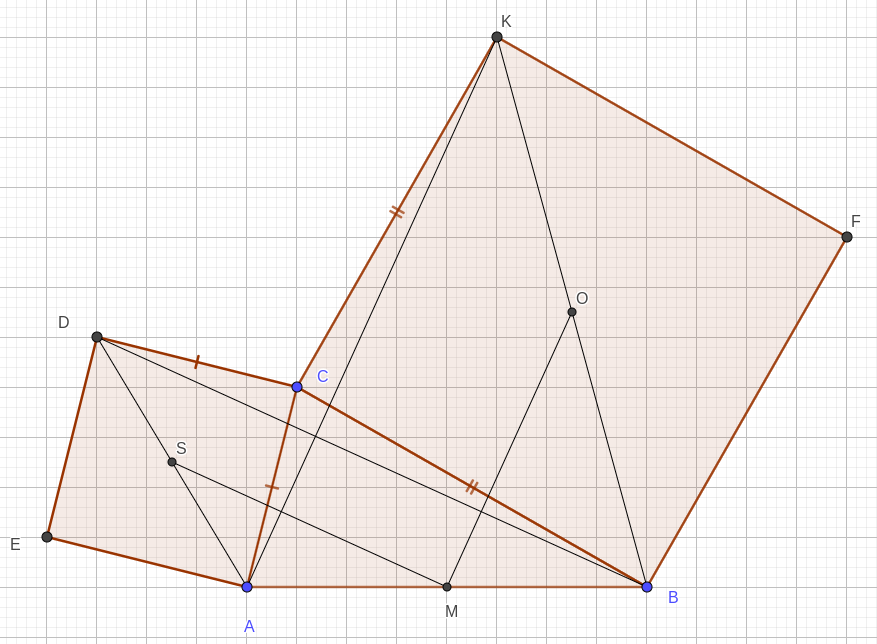
Рассмотрим треугольник \(ACK\). В нём \(\angle C = 90^\circ + 30^\circ = 120^\circ\) и сторону \(AK\) можно найти по теореме косинусов: $$ AK^2 = AC^2 + CK^2 - 2 \cdot AC \cdot CK \cos 120^\circ = $$ $$ = 10^2 + 32^2 - 2 \cdot 10 \cdot 32 \cdot \left( - \frac{1}{2} \right) = $$ $$ = 100 + 1024 + 320 = 1444 $$ Значит, \(AK = \sqrt{1444} = 38\) и \(MO = 19\).

Пусть \(S\) - центр квадрата \(CDEA\). Чтобы найти \(MS\), нужно рассмотреть треугольник \(ADB\). В нём \(MS\) - средняя линия и \(MS = \dfrac{1}{2} DB\). Рассмотрим треугольник \(DCB\). Он равен треугольнику \(ACK\) (у них равны две стороны \(CD = CA\), \(CB = CK\) и углы между ними \(\angle ACB = \angle ACK\). Поэтому, \(DB = 38\), \(MS = 19\).

Ответ: б) \(19\).