Решение:

а) Пусть \(O\) - точка пересечения диагоналей параллелограмма \( ABCD \). Так как \( AD \) - диаметр окружности, проходящей через \( O \), то треугольник \( AOD \) - прямоугольный, \( \angle AOD = 90^\circ \). Значит диагонали параллелограмма \( ABCD \) пересекаются под прямым углом, поэтому \( ABCD \) - ромб.

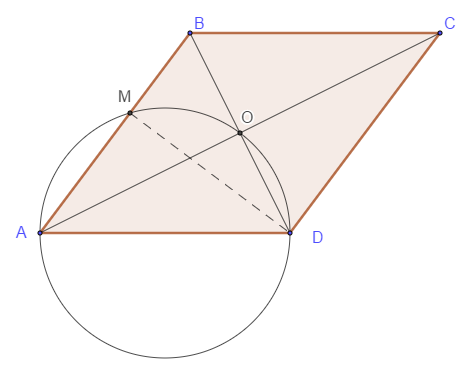
б) \( AM = \dfrac{1}{3} AB = \dfrac{1}{3} AD = \dfrac{2 \sqrt{3}}{3} \). Треугольник \( AMD \) - прямоугольный. $$ \cos \angle MAD = \dfrac{AM}{AD} = \dfrac{1}{3}. $$ Далее, \( \angle MAD = 2 \angle OAD \) (диагонали ромба являются биссектрисами его углов). Поэтому, $$ \cos^2 \angle OAD = \frac{\cos \angle MAD + 1}{2} = \frac{2}{3}, \quad \Rightarrow \quad \cos \angle OAD = \sqrt{\frac{2}{3}}. $$ $$ AO = AD \cos \angle OAD = 2 \sqrt{3} \cdot \frac{\sqrt{2}}{\sqrt{3}} = 2 \sqrt{2} \quad \Rightarrow \quad AC = 2 \cdot AO = 4 \sqrt{2}. $$

Ответ: б) \(4 \sqrt{2}\).