Решение:

а) Обозначим \( \angle LBC = \angle LBA = \angle LDB =\alpha \). Тогда \( \angle ABC = \angle ACB = 2 \alpha \). Угол \( ACB \) - внешний для треугольника \( DCL \). Поэтому \( 2 \alpha = \angle LCB = \angle CLD + \angle CDL = \angle CLD + \alpha \). Поэтому \( \angle CLD = \angle CDL = \alpha \) и, значит, треугольник \( DCL \) - равнобедренный.

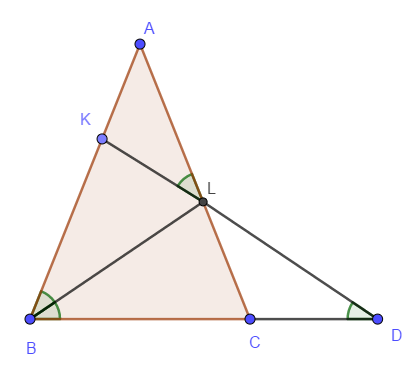
б) Так как \( \cos \angle ABC = \dfrac{3}{4} \), то \( AB : BC = 2 : 3 \). Пусть \( AB = 2x\), \( BC = 3x \). Из того, что \( BL \) - биссектриса, следует, что \( AL : LC = 2 : 3 \), т.е. \( 2z + 3z = 2x \), \( z = \dfrac{2x}{5} \), \( AL =\dfrac{2}{5} AB \).

\( \angle ALK = \angle CLD = \alpha \) как вертикальные. Отсюда треугольники \( ALK \) и \(ABL \) подобны по двум углам (угол \( A \) - общий). Поэтому \( \dfrac{AL}{AB} = \dfrac{AK}{AL} \), значит \( AL^2 = AB \cdot AK \) $$ \frac{4}{25} \cdot AB^2 = AB \cdot AK \quad \Rightarrow \quad AK = \frac{4}{25} AB $$ $$ BK = \left( 1 - \frac{4}{25} \right) AB = \frac{21}{25} AB $$ Поэтому \( AK : BK = 4 : 21 \).

Ответ: б) \( 4 : 21 \).