Задание 17. Вариант 5
- Просмотры: 264
- Изменено: 1 февраля 2025
Точки \( B_1 \) и \( C_1 \) лежат на сторонах соответственно \( AC \) и \( AB \) треугольника \( ABC, \) причём \( AB_1 : B_1 C = AC_1 : C_1 B . \) Прямые \( BB_1 \) и \( CC_1 \) пересекаются в точке \( O. \)
а) Докажите, что прямая \( AO \) делит пополам сторону \( BC. \)
б) Найдите отношение площади четырёхугольника \( AB_1OC_1 \) к площади треугольника \( ABC, \) если известно, что \( AB_1 : B_1 C = AC_1 : C_1 B = 1 : 3.\)
Решение:
а) Будем обозначать расстояние от точки \( X \) до прямой \( YX \) как \( h_{X,YZ} \).
Тогда $$ \frac{2S_{AOB}}{2S_{AOC}} = \frac{2S_{AA_1B} - 2S_{BOA_1}}{2S_{AC_1C} - 2S_{AOC_1}} = \frac{BA_1 \cdot h_{A,BC} - BA_1 \cdot h_{O,BC}}{A_1C \cdot h_{A,BC} - A_1 C \cdot h_{O,BC}} = \frac{BA_1}{A_1 C} $$ $$ \frac{2S_{AOC}}{2S_{BOC}} = \frac{2S_{ACC_1} - 2S_{AC_1O}}{2S_{BCC_1} - 2S_{BOC_1}} = \frac{AC_1 \cdot h_{C,AB} - AC_1 \cdot h_{O,AB}}{C_1B \cdot h_{C,AB} - C_1 B \cdot h_{O,AB}} = \frac{AC_1}{C_1 B} $$ $$ \frac{2S_{BOC}}{2S_{AOB}} = \frac{2S_{BB_1C} - 2S_{B_1OC}}{2S_{ABB_1} - 2S_{AOB_1}} = \frac{CB_1 \cdot h_{B,AC} - CB_1 \cdot h_{O,AC}}{B_1 A \cdot h_{B,AC} - B_1 A \cdot h_{O,AC}} = \frac{CB_1}{B_1 A} $$ Перемножая правые и левые стороны этих равенств, получаем $$ 1 = \frac{AC_1}{C_1B} \frac{BA_1}{A_1C} \frac{CB_1}{B_1A} $$ Но из условия задачи следует, что $$ \frac{AC_1}{C_1B} \frac{CB_1}{B_1A} = 1 $$ Поэтому $$ \frac{BA_1}{A_1C} = 1 \quad \Rightarrow \quad BA_1 = CA_1 $$
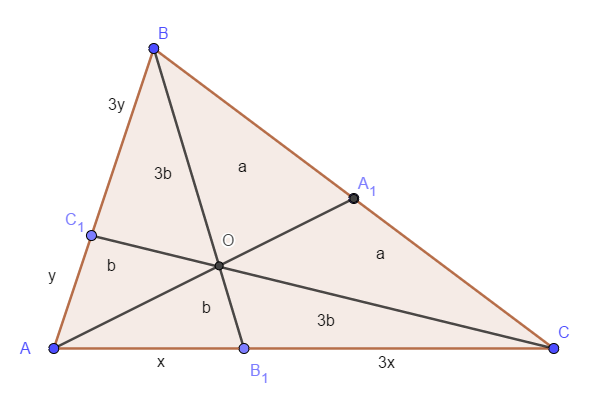
б) Пусть \( AB_1 = x \), \( AC_1 = y \). Тогда \( B_1 C = 3 x \), \( C_1 B = 3y \). Далее, \( AA_1 \) - медиана треугольника \( ABC \) и \( OA_1 \) - медиана треугольника \( OBC \). Поэтому \( S_{BOA_1} = S_{COA_1} = a \), где \( a \) - некоторое число.
Так как \( S_{AA_1B} = S_{AA_1C} \), то \( S_{AOB} = S_{AOC} \). Отсюда $$ AB \cdot h_{O,AB} = AC \cdot h_{O, AC} \quad \Rightarrow \quad 4y \cdot h_{O,AB} = 4x \cdot h_{O,AC} \quad \Rightarrow \quad h_{O,AB} = \frac{x}{y} \cdot h_{O,AC} $$ Значит $$ S_{AOC_1} = \frac{1}{2} y \cdot h_{O,AB} = \frac{1}{2} y \cdot \frac{x}{y} \cdot h_{O,AC} = \frac{1}{2} x \cdot h_{O,AC} = S_{AOB_1} $$ Пусть \( S_{AOC_1} = S_{AOB_1} = b \), тогда \( S_{C_1OB} = S_{B_1OC} = 3b. \) Теперь, $$ S_{AB_1OC_1} = 2b, \qquad S_{ABC} = 8b + 2a. $$
Так как \( S_{BCC_1} = 3 S_{ACC_1} \), то $$ 3b + 2a = 3 \cdot 5b \quad \Rightarrow \quad 2a = 12 b. $$ Окончательно, $$ \frac{S_{AB_1OC_1}}{S_{ABC}} = \frac{2b}{8b + 2a} = \frac{2b}{20b} = \frac{1}{10} $$
Ответ: б) \( \dfrac{1}{10} \).