Задание 17. Вариант 12
- Просмотры: 38
- Изменено: 2 декабря 2024
Окружность с центром \( O \), вписанная в прямоугольный треугольник \( ABC \), касается гипотенузы \( AB \) в точке \( M \), а катета \( AC \) — в точке \( N \), \( AC < BC\). Прямые \( MN \) и \( CO \) пересекаются в точке \( K \).
а) Докажите, что угол \( CKN \) в два раза меньше угла \( ABC \).
б) Найдите \( BK \), если \( BC = 3 \sqrt{2} \).
Решение:
а) Треугольник \( AMN \) — равнобедренный. Поэтому \( \angle ANM = \dfrac{180^\circ - \angle A}{2} \). С другой стороны, \( \angle ANM \) — внешний угол треугольника \( KCN \). Поэтому $$ \angle CKN = \angle ANM - \angle NCK = \frac{180^\circ - \angle A}{2} - \frac{\angle C}{2} = \frac{\angle ABC}{2}, $$ так как \( CK \) — биссектриса.
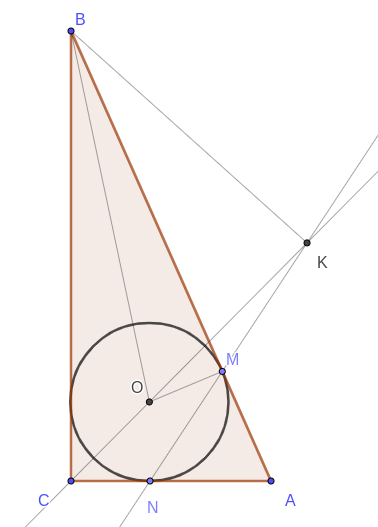
б) Так как \( \angle OBM= \angle OKM \), то точки \( O \), \( B \), \( K \) и \( M \) лежат на одной окружности. Треугольник \( BOM \) — прямоугольный. Поэтому треугольник \( OBK \) тоже прямоугольный с прямым углом \( K \). Значит \( BK = BC \sin 45^\circ = 3\).
Ответ: б) \( 3 \).