Решение:

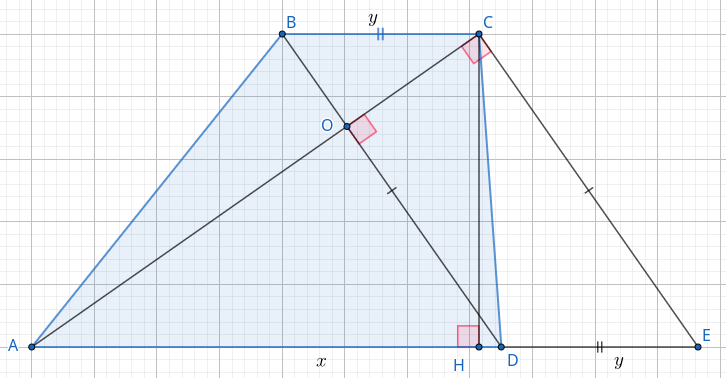
а) Пусть \(ABCD\) — трапеция с основаниями \(AD = x\) и \(BC = y.\) Пусть \(AC = 15\) и \(BD = 8.\) Продлим основание \(AD\) за точку \(D\) до точки \(E\) так, что \(DE = BC = y.\) Так как с другой стороны \(DE \parallel BC,\) то \(DBCE\) — параллелограмм. Значит \(BD \parallel CE\) и \(CE = BD = 8.\) Кроме того, \(AE = x + y = 17.\) Получаем, что $$AC^2 + CE^2 = 15^2 + 8^2 = 17^2 = AE^2.$$ Значит \(\triangle ACE\) прямоугольный по обратной теореме Пифагора. Т.е. \(AC \perp CE.\) А так как \(BD \parallel CE,\) то \(AC \perp BD.\) Ч.т.д.

б) Высота \(CH\) трапеции является высотой прямоугольного треугольника \(ACE,\) опущенной из вершины прямого угла \(C\) на гипотенузу \(AE.\) Рассмотрим площадь этого треугольника: $$S_{ACE} = \frac{1}{2} CH \cdot AE = \frac{1}{2} AC \cdot CE.$$ Отсюда $$CH = \frac{AC \cdot CE}{AE} = \frac{8 \cdot 15}{17} = \frac{120}{17}.$$

Ответ: б) \(\cfrac{120}{17}\)