Решение:

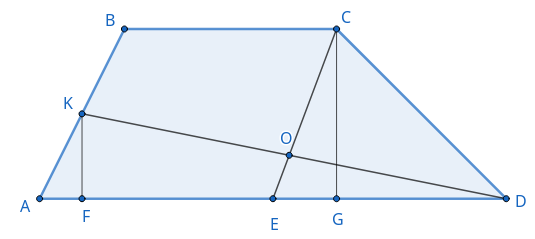
а) Пусть \(h\) — высота трапеции \(ABCD.\) \((CG = h)\) Тогда перпендикуляр \(KF\), опущенный из точки \(K\) на основание \(AD,\) равен \(\cfrac{h}{2}.\) Получаем, что $$S_{AKD} = \cfrac{1}{2} \cdot \cfrac{h}{2} \cdot AD = \frac{1}{2} \cdot h \cdot \frac{AD}{2} = S_{CED}.$$ А так как \(S_{AKD} = S_{AKOE} + S_{EOD}\) и \(S_{CED} = S_{COD} + S_{EOD}\) заключаем, что \(S_{AKOE} = S_{COD}.\)

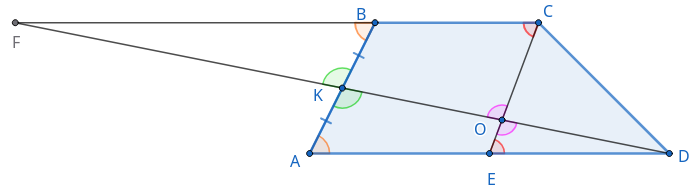
б) Продолжим отрезки \(DK\) и \(CB\) до их пересечения в точке \(F.\) Имеем \(\angle FBK = \angle DAK\) как накрест лежащие при параллельных прямых \(FB\) и \(AD\) и секущей \(AB.\) Кроме того, \(\angle FKB = \angle DKA\) как вертикальные. Учитывая, что по условию задачи \(AK = BK\) заключаем, что \(\triangle FKB = \triangle DKA,\) а значит \(FB = AD = 4\) и \(FC= FB + BC = 7.\) Теперь \(\angle FCO = \angle DEO\) как накрест лежащие при параллельных прямых \(FC\) и \(ED\) и секущей \(CE.\) Также \(\angle EOD = \angle COF\) как вертикальные. Делаем вывод, что \(\triangle FCO \sim \triangle DEO.\) Отсюда $$\frac{CO}{EO} = \frac{FC}{ED} = \frac{7}{2} \, \Rightarrow \, \frac{CO}{CE} = \frac{7}{9} \Rightarrow \frac{S_{COD}}{S_{CED}} = \frac{7}{9}$$ Но \(S_{CED} = \cfrac{1}{2} \cdot h \cdot ED = h.\) Значит, \(S_{COD} = \cfrac{7}{9} h.\) Площадь же самой трапеции \(ABCD\) равна $$S_{ABCD} = \frac{AD + BC}{2} \cdot h = \frac{7}{2} \cdot h.$$ Значит $$\frac{S_{AKOE}}{S_{ABCD}} = \frac{S_{COD}}{S_{ABCD}} = \frac{7h}{9} \cdot \frac{2}{7 h} = \frac{2}{9}.$$

Ответ: б) \(\cfrac{2}{9}\)