Решение:

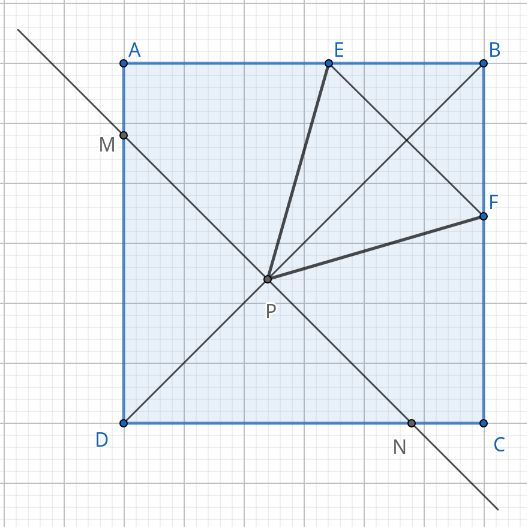
а) Прямая, проходящая через точку \(P\) и отрезок \(EF\) лежат по разные стороны от диагонали \(AC,\) иначе четырёхугольник \(EBPF\) выродится в треугольник \(EBF.\) Так как \(BE = BF,\) то \(EF \perp BD.\) Пусть сторона квадрата \(AB = a.\) Тогда $$S_{EBFP} = \frac{1}{2} BP \cdot EF = \frac{1}{2} BP \cdot \sqrt{2} BE = \frac{\sqrt{2}}{2} BP \cdot BE = \frac{a^2}{3}$$ И если \(BP \cdot BE = \sqrt{2},\) то \(\cfrac{a^2}{3} = 1.\) Значит \(a = AB = \sqrt{3}.\)

б) Пусть прямая, параллельная \(AC\) и проходящая через точку \(P\) пересекает стороны квадрата \(DA\) и \(DC\) в точках \(M\) и \(N\) соответственно. Тогда, \(DM = DN\) (по теореме Фалеса). Значит $$S_{DMN} = \frac{DM^2}{2} = \frac{a^2}{3} \Rightarrow DM = \frac{a \sqrt{2}}{\sqrt{3}}$$ Далее, \(BD = a \sqrt{2},\) \(DP = DM \cos 45^\circ = \cfrac{a \sqrt{2}}{\sqrt{3}} \cdot \cfrac{\sqrt{2}}{2} = \cfrac{a}{\sqrt{3}}.\) Значит, \(BP = a \sqrt{2} - \cfrac{a}{\sqrt{3}} = a \left( \sqrt{2} - \cfrac{1}{\sqrt{3}} \right).\) Пусть \(EB = x,\) тогда \(EF = x \sqrt{2}\) и $$S_{EBFP} = \frac{1}{2} BP \cdot EF = ax \frac{\sqrt{2}}{2} \left( \sqrt{2} - \frac{1}{\sqrt{3}} \right) = \frac{a^2}{3}$$ Отсюда $$x = \frac{a \sqrt{6}}{3 (\sqrt{6} - 1)} .$$ Площади треугольников \(EBF\) и \(EPF\) равны соответственно $$S_{EBF} = \frac{1}{2} x^2 = \frac{a^2}{3 (\sqrt{6} - 1)^2}$$ $$S_{EPF} = \frac{a^2}{3} - \frac{a^2}{3 (\sqrt{6} - 1)^2} = a^2 \left( \frac{(\sqrt{6} - 1)^2 - 1}{3 (\sqrt{6} - 1)^2} \right)$$ Отсюда $$\frac{S_{EPF}}{S_{EBF}} = (\sqrt{6} - 1)^2 - 1 = 6 - 2 \sqrt{6}$$

Ответ: \(6 - 2 \sqrt{6}\)