Решение:

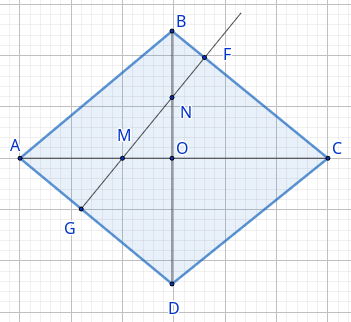
а) Пусть прямая \(MN\) пересекает сторону \(BC\) в точке \(F.\) Из условия задачи получаем: \(AM = \cfrac{1}{3} AC = \cfrac{2}{3} AO,\) \(MO = \cfrac{1}{3} AO,\) \(BN = \cfrac{1}{4} BD = \cfrac{1}{2} BO = NO.\) Далее, \(\triangle BFN \sim \triangle BOC\) по двум углам: они прямоугольные и угол \(B\) у них общий. Поэтому \(\angle BCO = \angle BNF.\) Теперь $$\cos \angle BCO = \frac{OC}{BC} = \frac{AC}{2 BC} = \frac{FC}{MC} = \frac{3 FC}{2 AC} \, \Rightarrow \, \cos^2 \angle BCO = \frac{3 FC}{4 BC}$$ $$\sin \angle BCO = \frac{BF}{BN} = \frac{4 BF}{BD} = \frac{BO}{BC} = \frac{BD}{2 BC} \, \Rightarrow \, \sin^2 \angle BCO = \frac{2 BF}{BC}$$ Учитывая, что \(BF + FC = BC,\) получаем $$1 = \frac{2 BF}{BC} + \frac{3 FC}{4 BC} = \frac{8 BF + 3 FC}{4 BC} = \frac{5 BF}{4 BC} + \frac{3}{4}$$ Отсюда $$\frac{BF}{BC} = \frac{1}{5} \, \Rightarrow \, FC = \frac{4}{5} BC \, \Rightarrow \, \frac{BF}{FC} = \frac{1}{4}.$$

б) $$\tan \angle BAO = \frac{BO}{AO} = \frac{MO}{NO} = \frac{2 AO}{3 BO} \, \Rightarrow \, 3 BO^2 = 2 AO^2.$$ С другой стороны, $$12 = MN^2 = MO^2 + NO^2 = \left( \frac{AO}{3} \right)^2 + \left( \frac{BO}{2} \right)^2 \, \Rightarrow \, 4 AO^2 + 9 BO^2 = 3 \cdot 12^2$$ Отсюда получаем, что $$AO^2 = \frac{3 \cdot 12^2}{10}, \,\, BO^2 = \frac{2 AO^2}{3} = \frac{12^2}{5},$$ $$AB^2 = AO^2 + BO^2 = \frac{3 \cdot 12^2}{10} + \frac{12^2}{5} = 2 \cdot 6^2 \, \Rightarrow \, AB = 6 \sqrt{2}$$

Ответ: б) \(6 \sqrt{2}\)