Решение:

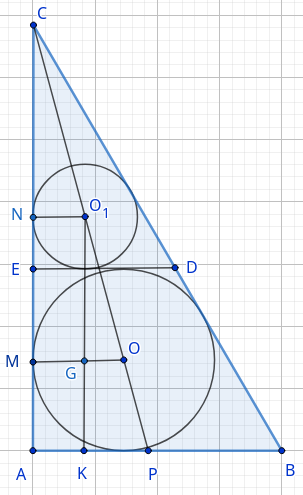
а) Прямая \(OC_1\) биссектриса угла \(ECD,\) а прямая \(CO\) — биссектриса \(\angle ACD = \angle ECD.\) Значит точки \(C, \, O_1, \, O, \, P\) лежат на одной прямой — биссектрисе угла \(ACD.\) Но тогда по свойству биссектрисы имеем $$\frac{AP}{BP} = \frac{CA}{CB} = \cos \angle ACB.$$

б) Обозначим \(\gamma = \angle ACB.\) Опустим из точек \(O\) и \(O_1\) перпендикуляры \(O_1N\) и \(OM\) на катет \(AC.\) Опустим также перпендикуляр \(O_1K\) из точки \(O_1\) на катет \(AB.\) И пусть \(OM\) и \(O_1K\) пересекаются в точке \(G.\) Тогда \(O_1 N = GM = AK = 3, \, OM = 5, \, OG = OM - GM = 2,\) \(O_1G = 3 + 5 = 8, \, O_1 K = 3 + 5 + 5 = 13.\) Далее, так как \(O_1 K \parallel AC,\) то \(\angle GO_1O = \cfrac{\gamma}{2}.\) Значит, \(\tan \cfrac{\gamma}{2} = \cfrac{OG}{O_1G} = \cfrac{1}{4}.\) Теперь, $$\tan^2 \frac{\gamma}{2} = \frac{\sin^2 \frac{\gamma}{2}}{\cos^2 \frac{\gamma}{2}} \, \Rightarrow \, \cos^2 \frac{\gamma}{2} = \frac{1}{1 + \tan^2 \frac{\gamma}{2}} = \frac{1}{1 + \frac{1}{16}} = \frac{16}{17}$$ $$\cos \gamma = 2 \cos^2 \frac{\gamma}{2} - 1 = \frac{32}{17} - 1 = \frac{15}{17}$$ Значит, \(AB : AC : BC = 8 : 15 : 17.\) Теперь $$PK = O_1K \tan \cfrac{\gamma}{2} = \cfrac{13}{4},$$ $$AP = AK + PK = 3 + \cfrac{13}{4} = \cfrac{25}{4},$$ $$PB = \frac{AP}{\cos \gamma} = \frac{25}{4} \cdot \frac{17}{15} = \frac{85}{12} \, \Rightarrow \, AB = \frac{25}{4} + \frac{85}{12} = \frac{40}{3} = 8 \cdot \frac{5}{3}$$ Отсюда \(AC = 15 \cdot \cfrac{5}{3} = 25,\) \(S_{ABC} = \cfrac{1}{2} \cdot 25 \cdot \cfrac{40}{3} = \cfrac{500}{3}= 166 \cfrac{2}{3}.\)

Ответ: б) \(166 \cfrac{2}{3}\)