Решение:

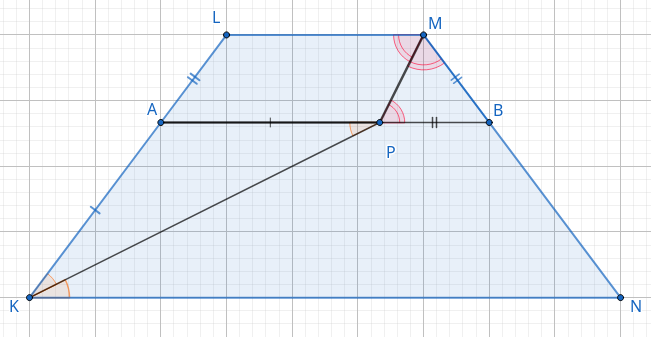
а) \(AB \parallel KN \, \Rightarrow \, \angle APK = \angle NKP\) как накрест лежащие при параллельных прямых. С другой стороны, по условию \(\angle NKP = \angle AKP.\) Значит, \(\triangle AKP\) равнобедренный: \(AK = AP.\) Аналогично доказывается, что \(\triangle MBP\) равнобедренный и \(BP = BM.\) Так как по условию \(AB = KL\) и из того, что \(AP = AK,\) делаем вывод, что \(AL = PB = BM.\) Но тогда из теоремы Фалеса следует, что $$\frac{AL}{MB} = \frac{AK}{BN} = 1,$$ т.е. \(AK = BN\) и значит \(KL = NM.\)

б) Пусть \(\angle LKN = \alpha.\) Тогда \(\angle KAP = 180^\circ - \alpha.\) Так как трапеция \(KLMN\) равнобедренная, то \(\angle KNB = \angle PBM = \alpha.\) Пусть \(AP = x,\) тогда \(BP = 2x.\) По теореме косинусов получаем следующие выражения: $$KP^2 = AK^2 + AP^2 - 2 \cdot AK \cdot AP \cdot \cos(180^\circ - \alpha) = x^2 + x^2 + 2x^2 \cos \alpha = 2x^2 (1 + \cos \alpha),$$ $$MP^2 = BP^2 + BM^2 - 2 \cdot BP \cdot BM \cdot \cos \alpha = 4x^2 + 4x^x - 8x^2 \cos \alpha = 8x^2 (1 - \cos \alpha).$$ Поэтому $$\frac{KP^2}{MP^2} = \frac{4}{9} = \frac{1 + \cos \alpha}{4 (1 - \cos \alpha)}.$$ Отсюда находим, что \(\cos \angle LKN = \cos \alpha = \cfrac{7}{25} = 0{,}28.\)

Ответ: б) \(0{,}28\)