Решение:

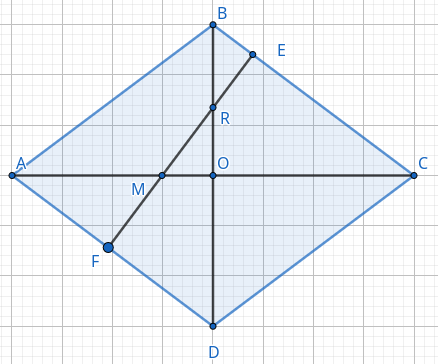
а) Из условия задачи получаем, что \(BE = \cfrac{1}{5} BC,\) \(EC = \cfrac{4}{5} BC,\) \(BR = RO = \cfrac{1}{2} BO.\) Пусть \(\cfrac{CM}{AM} = k.\) Тогда получаем, что \(CM = k \cdot AM, \) \(AC = 2 OC = (k + 1) AM.\) Отсюда $$AM = \frac{2 OC}{k + 1}, \,\, MC = 2OC - AM = \frac{2k \cdot OC}{k + 1}.$$ Далее, \(\triangle BRE \sim \triangle BCO\) (они прямоугольные с общим острым углом \(B\)), \(\triangle BRE \sim \triangle MRO\) (они прямоугольные и \(\angle BRE = \angle MRO\) как вертикальные). Обозначим \(\angle BCO\) через \(\gamma.\) Тогда $$\sin \gamma = \frac{BE}{BR} = \frac{2BC}{5BO} = \frac{BO}{BC} \, \Rightarrow \, \frac{BO^2}{BC^2} = \sin^2 \gamma = \frac{2}{5} \, \Rightarrow \, \cos^2 \gamma = \frac{3}{5}.$$ $$\cos \gamma = \frac{EC}{MC} = \frac{4 BC}{5 MC} = \frac{4 (k+1) BC}{5 \cdot 2k OC} = \frac{OC}{BC} \, \Rightarrow \, \frac{OC^2}{BC^2} = \frac{2(k+1)}{5k} = \frac{3}{5}$$ То есть \(2(k+1) = 3k.\) Значит \(k = 2,\) ч.т.д.

б) Так как \(\cfrac{BO^2}{BC^2} = \cfrac{2}{5},\) то \(5BO^2 = 2BC^2.\) Теперь $$MO^2 + OR^2 = MR^2 = 12 \, \Rightarrow \, \frac{OC^2}{9} + \frac{BO^2}{4} = 12$$ $$4 (BC^2 - BO^2) + 9BO^2 = 12 \cdot 36 \, \Rightarrow \, 4BC^2 + 5BO^2 = 12 \cdot 36 \, \Rightarrow \,6BC^2 = 3 \cdot 12^2.$$ Отсюда \(BC = 6 \sqrt{2},\) \(P_{ABCD} = 4 BC = 24 \sqrt{2}.\)

Ответ: б) \(24 \sqrt{2}\)