Решение:

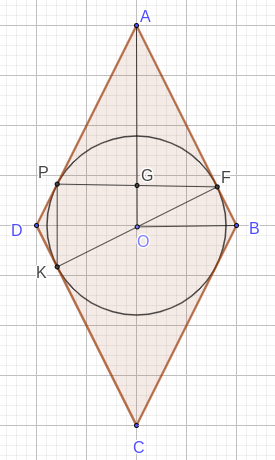
а) \(AP = AF\) как касательные к окружности, проведённые из одной точки. Тогда \(\Delta APF\) равнобедренный, значит \(AG \perp PF\) (\(G\) — середина \(PF\)). Далее, \(OP = OF\) как радиусы. Значит \(\Delta OPF\) равнобедренный, поэтому \(OG \perp PF\). Отсюда \(O\), \(G\) и \(A\) лежат на одной прямой, причём \(AO \perp PF\) и \(AO \perp BD\), значит \(PF \parallel BD.\) Аналогично можно доказать, что \(PK \parallel AC.\)

б) \(\Delta KFP\) прямоугольный, поэтому \(KF = \sqrt{KP^2 + PF^2} = \sqrt{6^2 + 8^2} = 10.\) Далее, \(\angle PFK = \angle BOF\) как накрест лежащие при параллельных прямых. Отсюда получаем, что \(\Delta FPK \sim \Delta OFB.\) Тогда $$\frac{OB}{FK} = \frac{OF}{FP} \Rightarrow \frac{x}{10} = \frac{5}{6}.$$ Значит, $$BD = 2 \cdot OB = \frac{2 \cdot 5 \cdot 10}{6} = \frac{50}{3}.$$ Теперь \(OF \perp AF\) и \(AO \perp PF.\) Отсюда \( \Delta AOF \sim \Delta FKP.\) Поэтому $$\frac{OA}{FK} = \frac{OF}{PK} \Rightarrow \frac{x}{10} = \frac{5}{8}.$$ Значит, $$AB = 2 \cdot OA = \frac{2 \cdot 5 \cdot 10}{8} = \frac{25}{2}.$$ Окончательно, площадь ромба \(ABCD\) равна $$S_{ABCD} = \frac{1}{2} AC \cdot BD = \frac{1}{2} \cdot \frac{50}{3} \cdot \frac{25}{2} = \frac{625}{6}$$

Ответ: \(\cfrac{625}{6}\)