Решение:

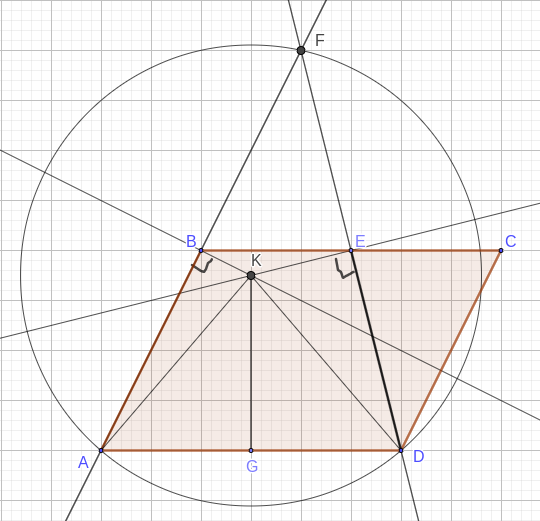
a) Продлим прямые \(AB\) и \(ED\) до их пересечения в точке \(F.\) Так как \(BE = \dfrac{1}{2} AD\) и \(BE \parallel AD,\) то \(BE\) — средняя линия треугольника \(AFD.\) Но тогда \(KB\) и \(KE\) — серединные перпендикуляры к сторонам \(AF\) и \(DF\) соответственно. Точка их пересечения \(K\) — центр описанной около \(\Delta AFD\) окружности. Но это означает, что \(AK = KD.\)

б) Пусть \(G\) — середина \(AD\). Тогда \(KG\) — серединный перпендикуляр к \(AD\). Получаем, что \(EC = BE = AG = GD = KG.\) (Последнее равенство следует из условия б)). Значит \(\Delta AGK = \Delta DGK,\) причём эти треугольники прямоугольные и равнобедренные. Но тогда \(\angle AKG = \angle DKG = 45^\circ ,\) а \(\angle AKD = 90^\circ .\) С другой стороны, \(\angle AKD\) центральный, который опирается на хорду \(AD\). Вписанный угол \(AFD\) опирается на ту же хорду, поэтому он равен \(45^\circ .\) Теперь, \(\angle BAD = 180^\circ - \angle ADC = 70^\circ,\) т.к. сумма углов параллелограмма, прилежащих одной стороне, равна \(180^\circ .\) Рассматривая теперь треугольник \(AFD\) окончательно получаем \(\angle BAD = 180^\circ - (45^\circ + 70^\circ ) = 65^\circ.\)

Ответ: б) \(65^\circ\)