Решение:

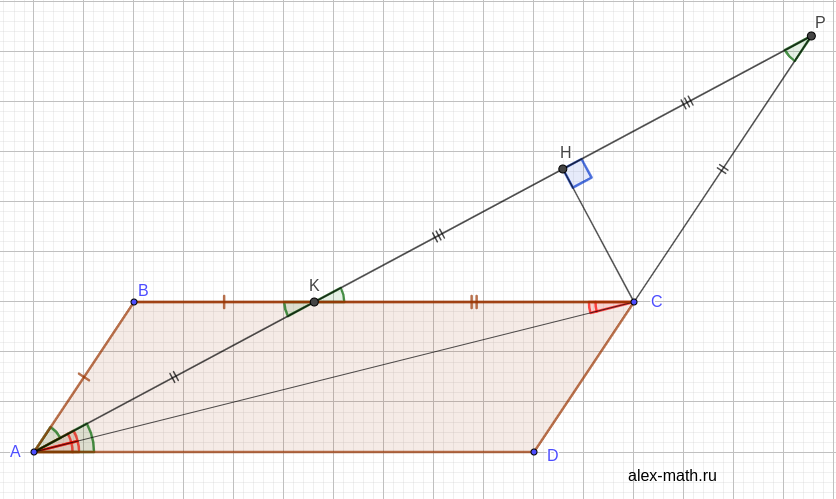
а) \(\angle BAK = \angle KAD\) по условию, \(\angle KAD = \angle BKA\) как накрест лежащие при параллельных прямых \(AD\) и \(BC.\) Поэтому \(\Delta ABK\) — равнобедренный \((AB = BK).\) Далее, \(\angle BKA = \angle CKP\) как вертикальные, \(\angle BAK = \angle CPK\) как накрест лежащие при параллельных прямых \(AB\) и \(PD.\) Поэтому \(\Delta ABK \sim \Delta PCK.\) Значит, \(PC : PK = AB : AK.\) Наконец, \(\angle KAC = \angle CAD\) по условию, \(\angle KCA = \angle CAD\) как накрест лежащие при параллельных прямых \(BC\) и \(AD.\) Значит, треугольник \(AKC\) равнобедренный и \(AK = KC.\) Отсюда \(AB : AK = CD : KC = CD : PC, \) Поэтому, \(PC^2 = CD \cdot PK.\)

б) \(BC : AB = 5 : 2 \Rightarrow AB = BK = 2x, \, CK = CP = 3x,\) где \(x\) — коэффиициент пропорциональности. Далее, \(AK : PK = AB : PC = 2 : 3 \Rightarrow PK = \cfrac{3}{2} AK = \cfrac{9x}{2}.\) Теперь, \(AC\) — биссектриса в \(\Delta PAD\), отсюда \(AD : AP = CD : CP \Rightarrow AP = \cfrac{AD \cdot CP}{ CD} = \cfrac{15x}{2}.\) В треугольнике \(CKP\) опустим высоту \(CH\) из вершины \(C\) на основание \(PK\). Тогда \(PH = HK = \cfrac{1}{2} (AP - AK) = \cfrac{9x}{4}.\) Чтобы найти \(AC\) два раза применим теорему Пифагора: $$CH^2 = PC^2 - PH^2 = 9x^2 - \frac{81 x^2}{16} = \frac{63x^2}{16},$$ $$AC^2 = AH^2 + CH^2 = (AK + KH)^2 + CH^2 = \left( 3x + \frac{9x}{4} \right)^2 + \frac{63x^2}{16} = \frac{504 x^2}{16}$$ Таким образом $$\frac{AC^2}{AP^2} = \frac{504x^2}{16} \cdot \frac{4}{225x^2} = \frac{14}{25} \Rightarrow \frac{AC}{AP} = \frac{\sqrt{14}}{5}.$$

Ответ: б) \(\cfrac{\sqrt{14}}{5}\)