Решение:

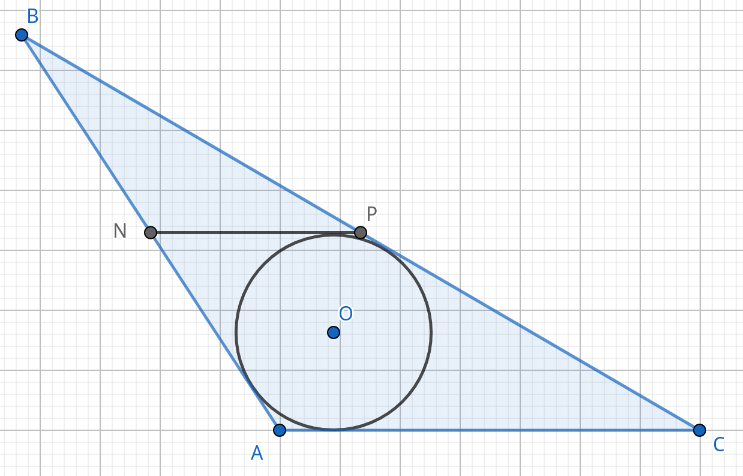
а) \(NP\) — средняя линия, значит \(2 NP = AC.\) По условию четырёхугольник \(ANPC\) описанный, значит \(AN + PC = NP + AC.\) Отсюда \(2AN + 2PC = AB + BC = 3 AC.\) Значит, \(P_{ABC} = AB + BC + AC = 3AC + AC = 4 AC.\)

б) \(P_{ABC} = 28 \Rightarrow AC = 7, \,\, AB + BC = 21, \Rightarrow BC = 21 - AB.\) По теореме косинусов $$(21 - AB)^2 = AB^2 + AC^2 - 2 \cdot AB \cdot AC \cdot \cos 120^\circ$$ $$21^2 - 42AB + AB^2 = AB^2 + 7^2 + 7AB \,\, \Rightarrow \,\, 49AB = 14 \cdot 28 \,\, \Rightarrow \,\, AB = 8$$ Значит \(S_{ABC} = \cfrac{1}{2} AB \cdot AC \cdot \sin 120^\circ = 14 \sqrt{3}. \)

Ответ: \(14 \sqrt{3}\)