Задание 17. Математика. ЕГЭ 2025. Ященко-8
- Просмотры: 54
- Изменено: 12 марта 2025
В треугольнике
- а) Докажите, что периметр треугольника
- б) Найдите площадь треугольника
Решение:
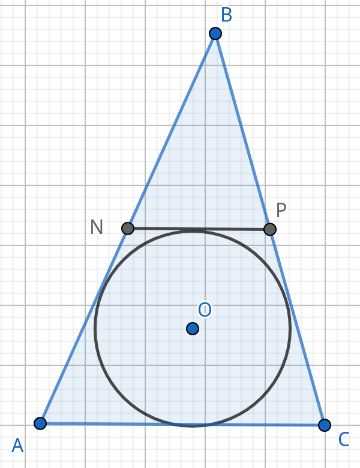
а)
б)
Ответ:
В треугольнике
Решение:

а)
б)
Ответ: