Решение:

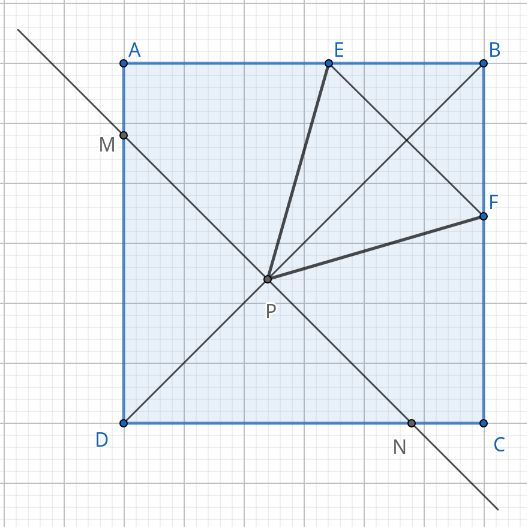
а) Прямая, проходящая через точку $P$ и отрезок $EF$ лежат по разные стороны от диагонали $AC,$ иначе четырёхугольник $EBPF$ выродится в треугольник $EBF.$ Так как $BE=BF,$ то $EF\perp BD.$ Пусть сторона квадрата $AB=a.$ Тогда $$S_{EBFP}=\frac{1}{2}BP\cdot EF=\frac{1}{2}BP\cdot \sqrt{2}BE=\frac{\sqrt{2}}{2}BP\cdot BE=\frac{a^2}{4}$$ И если $BP\cdot BE=\sqrt{2},$ то $\frac{a^2}{4}=1.$ Значит $a=AB=2.$

б) Пусть прямая, параллельная $AC$ и проходящая через точку $P$ пересекает стороны квадрата $DA$ и $DC$ в точках $M$ и $N$ соответственно. Тогда, $DM=DN$ (по теореме Фалеса). Значит $$S_{DMN}=\frac{D{M}^2}{2}=\frac{a^2}{4}\Rightarrow DM=\frac{a}{\sqrt{2}}$$ Далее, $BD=a\sqrt{2},$ $DP=DM\cos {45}^{\circ }=\frac{a}{\sqrt{2}}\cdot \frac{\sqrt{2}}{2}=\frac{a}{2}.$ Значит, $BP=a\sqrt{2}-\frac{a}{2}=a(\sqrt{2}-\frac{1}{2}).$ Пусть $EB=x,$ тогда $EF=x\sqrt{2}$ и $$S_{EBFP}=\frac{1}{2}BP\cdot EF=ax\frac{\sqrt{2}}{2}(\sqrt{2}-\frac{1}{2})=\frac{a^2}{4}$$ Отсюда $$x=\frac{a}{4-\sqrt{2}}.$$ Площади треугольников $EBF$ и $EPF$ равны соответственно $$S_{EBF}=\frac{1}{2}{x}^2=\frac{a^2}{2(4-\sqrt{2}{)}^2}$$ $$S_{EPF}=\frac{a^2}{4}-\frac{a^2}{2(4-\sqrt{2}{)}^2}=a^2\left(\frac{(4-\sqrt{2}{)}^2-2}{4(4-\sqrt{2}{)}^2}\right)$$ Отсюда $$\frac{S_{EPF}}{S_{EBF}}=\frac{(4-\sqrt{2}{)}^2-2}{2}=\frac{16-8\sqrt{2}}{2}=4(2-\sqrt{2})$$

Ответ: $4(2-\sqrt{2})$