Задание 17. Математика. ЕГЭ. Статград. 11.02.2025-1
- Просмотры: 391
- Изменено: 12 февраля 2025
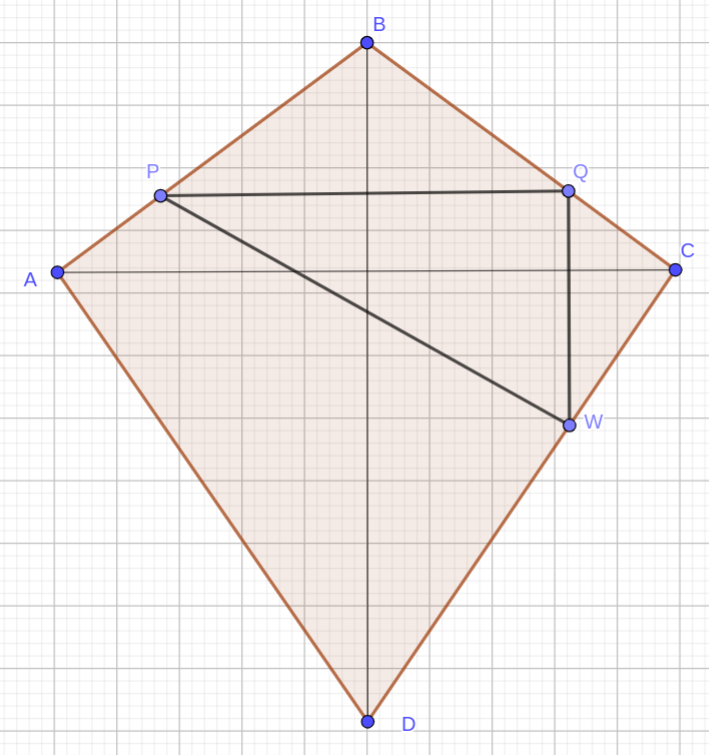
Точки \(P, \, Q, \, W\) делят стороны выпуклого четырёхугольника \(ABCD\) в отношении \(AP : BP = CQ : QB = CW : WD = 1 : 3.\) В треугольнике \(PQW\) угол \(W\) острый, при этом радиус описанной около этого треугольника окружности равен \(\cfrac{5}{4}\), \(PQ = 2,\) \(QW = \cfrac{3}{2}.\)
- а) Докажите, что треугольник \(PQW\) прямоугольный.
- б) Найдите площадь четырёхугольника \(ABCD.\)
Решение:
а) Первый вариант доказательства (короткий)
По теореме синусов $$\sin \angle W = \frac{4}{5}, \quad \sin \angle P = \frac{3}{5}.$$ Так как \(\angle W < 90^\circ ,\) то \(\cos \angle W = \cfrac{3}{5}.\) Т.е. \(\sin \angle P = \cos \angle W.\) А это означает, что \(\angle Q = 90^\circ .\)
Второй вариант доказательства (длинный)
По теореме синусов $$PW = 2 R \sin \angle Q = \frac{5}{2} \sin \angle Q$$ С другой стороны, из теоремы косинусов получаем, что $$PW^2 = PQ^2 + QW^2 - 2 \cdot PQ \cdot QW \cdot \cos \angle Q$$ $$\frac{25}{4} \sin^2 \angle Q = 4 + \frac{9}{4} - 6 \cos \angle Q = \frac{25}{4} - 6 \cos \angle Q$$ $$\sin^2 \angle Q = 1 - \frac{24}{25} \cos \angle Q \Rightarrow 1 - \cos^2 \angle Q = 1 - \frac{24}{25} \cos \angle Q$$ $$\cos \angle Q \left( \cos \angle Q - \frac{24}{25} \right) = 0$$ Значит, либо \(\cos \angle Q = 0\), либо \(\cos \angle Q = \cfrac{24}{25}.\)Рассмотрим второй случай. Тогда $$\sin^2 \angle Q = 1 - \frac{24^2}{25^2} \Rightarrow \sin \angle Q = \frac{7}{25} \Rightarrow PW = \frac{5}{2} \cdot \frac{7}{25} = \frac{7}{10}$$ Из теоремы косинусов для стороны \(PQ\) тогда получаем $$2 PW \cdot QW \cdot \cos \angle W = PW^2 + QW^2 - PQ^2 = \frac{49}{100} + \frac{9}{4} - 4 < 0$$ Т.е. \(\cos \angle W < 0,\) но это противоречит условию задачи. Значит \(\cos \angle W = 0,\) поэтому \(\angle W = 90^\circ .\)
б) \(\Delta CBD \sim \Delta CQW\) по двум сторонам и углу между ними (у них угол \(C\) общий, и \(CQ : CB = CW : CD = 1 : 3).\) Значит \(\angle CQW = \angle CBD.\) Поэтому \(BD \parallel QW.\) Аналогично доказывается, что \(PQ \parallel AC.\) Отсюда получаем, что \(BD = 3 QW = \cfrac{9}{2},\) \(AC = 3 PQ = 6.\) Угол между ними прямой. Поэтому, площадь четырёхугольника \(ABCD\) равна $$ S_{ABCD} = \frac{1}{2} AC \cdot BD = \frac{27}{2} $$
Ответ:б) \(\cfrac{27}{2}\)