Решение:

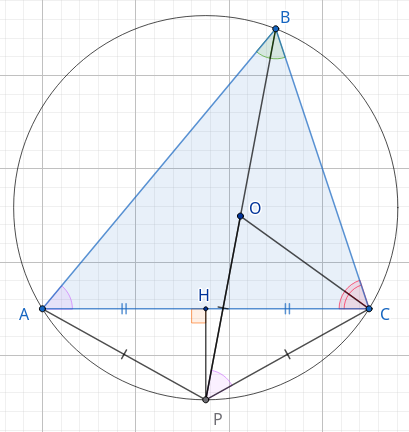
а)(Лемма о трезубце) Точка \(O\) — центр вписанной окружности, значит \(BO\) и \(CO\) биссектрисы соответствующих углов. Так как \(\angle ABP = \angle CBP,\) то и хорды, на которые они опираются равны: \(AP = CP.\) Обозначим углы в треугольнике \(ABC\) как \(\alpha =\angle A,\) \(\beta = \angle B,\) \(\gamma = \angle C.\) Угол \(BPC\) равен углу \(BAC,\) как вписанные и опирающиеся на одну и ту же хорду. Теперь \(\angle POC = \cfrac{\beta}{2} + \cfrac{\gamma}{2},\) как внешний угол для треугольника \(BOC.\) С другой стороны, \(\angle ACP = \angle ABP = \cfrac{\beta}{2}\) как вписанные углы, опирающиеся на одну и ту же хорду. Поэтому \(\angle PCO = \angle PCA + \angle ACO = \cfrac{\beta}{2} + \cfrac{\gamma}{2}.\) Значит, \(\angle POC = \angle PCO,\) поэтому \(OP = CP = AP.\)

б)\(\Delta PAC\) равнобедренный. Поэтому высота \(PH\) является также медианой и биссектрисой. Четырёхугольник \(PABC\) вписанный, значит \(\angle APC = 180^\circ - \angle ABC = 180^\circ - 60^\circ = 120^\circ .\) Откуда \(\angle APH = 60^\circ.\) Получаем, что \(AH = PH \tan 60^\circ = 24 \sqrt{3}.\) Отсюда \(AC = 2 AH = 48 \sqrt{3}.\) По теореме синусов $$\frac{AC}{\sin 60^\circ} = 2R \, \Rightarrow \, R = 48.$$

Ответ: \(48\)