Решение:

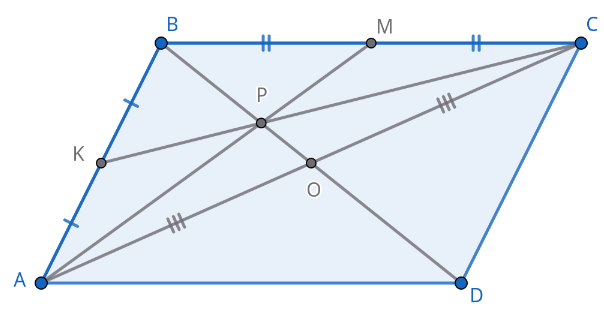
а) Проведём диагональ \(AC\) и рассмотрим треугольник \(ABC.\) В нём \(AM\) и \(CK\) — медианы. Пусть диагональ \(BD\) параллелограмма \(ABCD\) пересекает другую его диагональ \(AC\) в точке \(O.\) Тогда по свойству диагоналей параллелограмма \(AO = CO,\) т.е. \(BO\) в треугольнике \(ABC\) — медиана, а значит она проходит через точку \(P\) — точку пересечения медиан \(AM\) и \(CK.\)

б) Так как медианы в треугольнике точкой пересечения делятся в отношении \(2:1,\) то сразу получаем, что \(BO = 6,\) а \(BD = 12.\). Рассмотрим \(\triangle BCD.\) Его полупериметр \(p = \cfrac{25 + 17 + 12}{2} = 27.\) По теореме Герона его площадь $$S_{BCD} = \sqrt{27 (27 - 25) (27 - 17) (27 - 12)} = \sqrt{3^4 \cdot 2^2 \cdot 5^2} = 9 \cdot 2 \cdot 5 = 90.$$ Тогда площадь параллелограмма \(S_{ABCD} = 2 \cdot 90 = 180.\)

Ответ: б) \(180\)