Задание 18. Вариант 3
- Просмотры: 98
- Изменено: 29 января 2025
Найдите все значения \( a \), при каждом из которых система $$ \begin{cases} \left| x^2 - x - 6 \right| = (y-1)^2 + x - 7, \\ 3y = 2x + a \end{cases} $$ имеет ровно один или два корня.
Решение:
Так как \(x^2 - x - 6 = (x+2)(x-3)\), то \(x^2 - x - 6 < 0\) при \(-2 < x < 3\) и \(x^2 - x - 6 \geqslant 0\) при \(x \leqslant -2\) или \(x \geqslant 3\).
Рассмотрим первое уравнение системы.
\(x \in ( - \infty; \, -2 ] \cup [3; \, + \infty )\): $$ x^2 - x - 6 = (y-1)^2 + x - 7 \quad \Rightarrow \quad (x-1)^2 = (y-1)^2 $$ На этом отрезке первое уравнение задаёт пару прямых: $$ y = x \qquad \mbox{и} \qquad y = 2 - x $$
\(x \in (-2; \, 3)\): $$ -x^2 +x + 6 = (y-1)^2 + x - 7 \quad \Rightarrow \quad x^2 + (y-1)^2 = 13 $$ На этом интервале это уравнение задает часть окружности, радиусом \(13\) с центром в точке \( (0; \, 1)\).
Второе уравнение системы задает бесконечное множество параллельных прямых с угловым коэффициентом \(k = 2/3\). В частности, при \(a = 0\) - это прямая \(y = 2/3 x\), проходящая через начало координат и точку \( (3; \, 2)\). Эта прямая не имеет пересечения с первой линией.
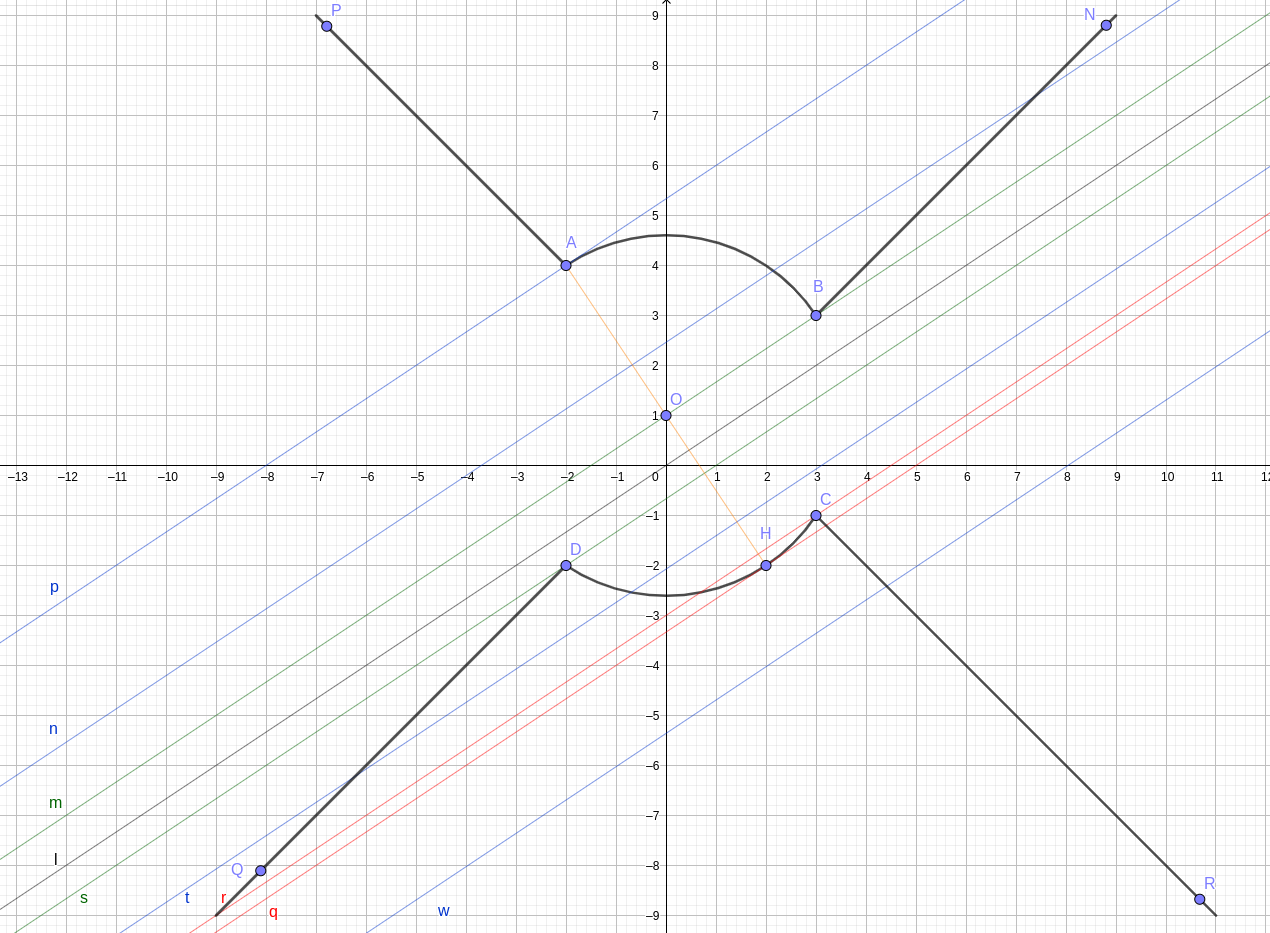
Исследуем пересечения прямой \( 3y = 2x + a\) с линией, задаваемой первым уравнением в зависимости от параметра \(a\). Начиная с \(a = 0\), когда пересечения нет начнем увеличивать \(a\). Когда прямая пройдёт через точку \(B(3; \, 3)\) - система имеет одно решение. Значение \(a\) найдём, подставив во второе уравнение координаты этой точки: $$ 3 \cdot 3 = 2 \cdot 3 + a \quad \Rightarrow \quad a = 3 $$ Случай \(a > 3\). Прямая \(3y = 2x + a\) касается дуги окружности в точке \(A (2; \, -4)\). Действительно, прямая \(OA\), на которой лежит радиус окружности, имеет угловой коэффициент \(k_1 = - 3/2\) и, поэтому \(k \cdot k_1 = -1\) и значит они перпендикулярны. Таким образом, при \(a > 3\) прямая \(3y = 2x + a\) пересекает линию, заданную первым уравнением в двух точках: одна лежит на луче \(BN\), вторая либо на дуге \(BA\), либо на луче \(AP\), а в точке \(A\) она касается дуги \(BA\) и эта же точка принадлежит лучу \(AP\).
Исследуем теперь случай отрицательных \(a\). Начнём уменьшать \(a\) с нуля до тех пор, пока прямая \(3y = 2x + a\) не пройдет через точку \(D (-2; \, -2)\). Найдём это значение \(a\): $$ 3 \cdot (-2) = 2 \cdot (-2) + a \quad \Rightarrow \quad a = -2 $$ При дальнейшем уменьшении \(a\) исследуемая прямая будет иметь два пересечения с кривой из первого уравнения, пока она не пройдёт через \(C( 3; \, -1)\). Здесь будет уже три пересечения. Значение \(a\) для этого случая: $$ 3 \cdot (-1) = 2 \cdot 3 + a \quad \Rightarrow \quad a = -9 $$ При последующем уменьшении \(a\) прямая второго уравнения будет пересекать кривую первого уравнения уже в четырёх точках до тех пор, пока не пройдёт через точку касания \(H\). Прямая \(OH\) должна в этом случае иметь угловой коэффициент \(k_1 = -3/2\), а так как квадрат радиуса дуги равен \(13 = 3^2 + 2^2\), то координаты точки \(H( 2; -2)\). Значение \(a\) в этом случае будет: $$ 3 \cdot (-2) = 2 \cdot 2 + a \quad \Rightarrow \quad a = -10 $$ При \(a < -10\) прямая второго уравнения опять будет пересекать кривую первого уравнения в двух точках.
Ответ: \(a \in (- \infty; \, -10) \cup ( -9; \, -2] \cup [3; \, + \infty )\).