Задание 18. Вариант 5
- Просмотры: 125
- Изменено: 31 января 2025
Решение:
Исследуем первое уравнение системы. Уравнение \( 2x^2 + y^2 -1 = 0 \) задаёт эллипс с центром в начале координат, который проходит через точки \( \left( \pm \frac{1}{\sqrt{2}}; 0 \right)\) и \( (0; \pm 1)\). Вне этого эллипса выражение, стоящее под модулем, больше нуля. Опуская знак модуля и приводя подобные, получаем уравнение \( x^2 + (y+1)^2 = \dfrac{3}{2} \). Оно задаёт окружность с центром в точке \( M(0; -1)\) и радиусом \( \sqrt{\dfrac{3}{2}} \). Так как $$ \left( \frac{1}{\sqrt{2}} \right)^2 + 1^2 = \frac{3}{2} $$ то окружность пересекает эллипс в точках \( C \left( \frac{1}{\sqrt{2}}; 0 \right)\) и \( D \left(- \frac{1}{\sqrt{2}}; 0 \right)\). Внутри эллипса \( 2x^2 + y^2 -1 < 0 \). Раскрывая модуль со знаком минус и приводя подобные получим уравнение \( y = \dfrac{1}{2} x^2 - \dfrac{1}{4} \). Это — парабола с вершиной в \( \left(0; - \dfrac{1}{4} \right) \).
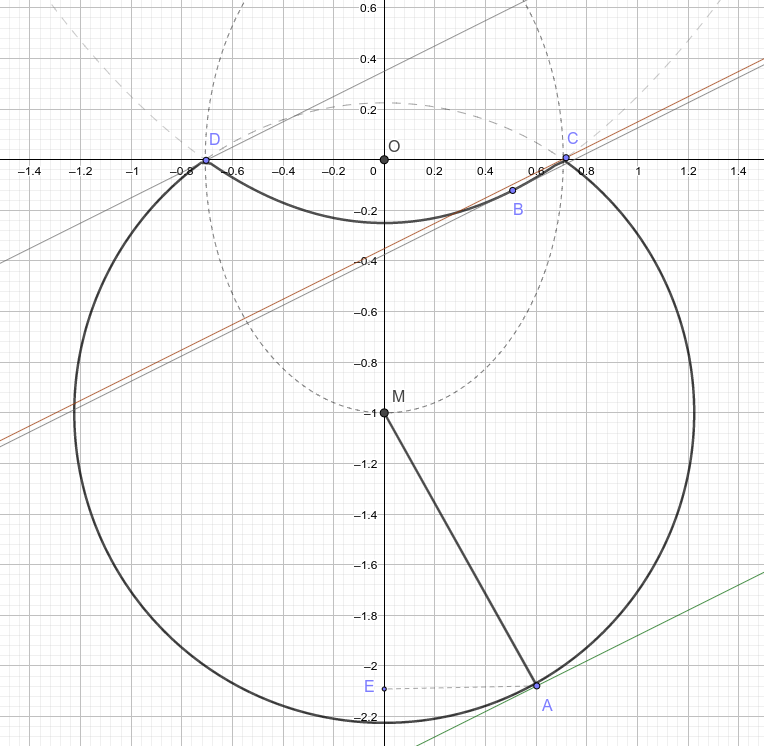
Второе уравнение \( y = \dfrac{1}{2}x + a \) задаёт семейство параллельных прямых с угловым коэффициентом \( \dfrac{1}{2} \). При больших по модулю отрицательных значениях \( a \) эта прямая не пересекается с кривой, задаваемой первым уравнением. Начнём увеличивать \( a\). При его определённом значении произойдёт касание в точке \( A \). Если \( k \) — угловой коэффициент прямой \( MA \), то тогда \( \dfrac{1}{2} \cdot k = -1 \), т.е. \( k = -2\). Другими словами, в прямоугольном треугольнике \( MAE \) тангенс угла \( A \) равен 2. Пусть \( ME = p\), \( AE = q \). Тогда $$ \frac{p}{q} = 2 \quad \Rightarrow \quad p = 2q. $$ С другой стороны $$ p^2 + q^2 = \frac{3}{2}.$$ Отсюда получаем, что \( p = 2 \sqrt{\dfrac{3}{10}} \), \( q = \sqrt{\dfrac{3}{10}} \) и, значит, точка \( A \) имеет координаты \( \left( \sqrt{\dfrac{3}{10}}; -1-2\sqrt{\dfrac{3}{10}} \right) \). Подставляя эти координаты во второе уравнение системы, находим, что \( a = -1 - \dfrac{\sqrt{30}}{4} \). При этом значении \(a\) система имеет одно решение. Продолжим увеличивать \( a \). У системы будет два решения. Это будет происходить до тех пор, пока прямая не коснётся параболы в точке \( B \). В этой точке значение производной \( y'=x \) функции \( y = \dfrac{1}{2}x^2 -\dfrac{1}{4} \) равно угловому коэффициенту \( \dfrac{1}{2} \) семейства прямых, задаваемому вторым уравнением системы. Т.е. координаты точки \( B \left( \dfrac{1}{2}; - \dfrac{1}{8} \right)\). Подставляя их во второе уравнение системы, находим, что \( a = - \dfrac{3}{8} \). При таком значении параметра \( a \) система имеет три решения. При дальнейшем увеличении \( a \) система имеет четыре решения, пока прямая второго уравнения не пройдёт через точку \( C \left( \dfrac{1}{\sqrt{2}}; 0 \right)\). Это даёт значение параметра \( a = - \dfrac{1}{2 \sqrt{2}} = - \dfrac{\sqrt{2}}{4} \), при котором система имеет три решения. Дальнейшее увеличение \( a \) приведёт к тому, что система будет иметь два решения до тех пор, пока прямая второго уравнения не пройдёт через точку \( D \left( -\dfrac{1}{\sqrt{2}}; 0 \right) \). Для неё \( a = \dfrac{\sqrt{2}}{4} \) и у системы одно решение. При большем значении \( a \) система решений не имеет.
Ответ: \( \left( -1 - \dfrac{\sqrt{30}}{4}; - \dfrac{3}{8} \right] \cup \left[ - \dfrac{\sqrt{2}}{4}; \dfrac{\sqrt{2}}{4} \right) \).