Задание 1. Информатика. ЕГЭ. Статград. 04.03.2025
- Просмотры: 1469
- Изменено: 5 апреля 2025
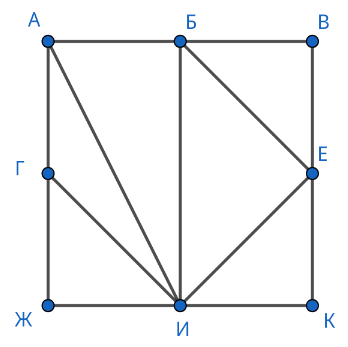
На рисунке схема дорог изображена в виде графа, в таблице звёздочкой отмечено наличие дороги между двумя населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация пунктов в таблице никак не связана с буквенными обозначениями на графе. Кроме того, при заполнении таблицы одну дорогу случайно пропустили.
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Определите два населённых пункта, дорога между которыми есть на графе, но не отмечена в таблице. В ответе запишите номера этих пунктов в таблице в порядке возрастания, без разделителей между ними, как двузначное число. Например, если бы в таблице была пропущена дорога между пунктами П1 и П2, в ответе следовало бы написать число \(12.\)
Решение:
Определим по графу степень вершин: А — \(3,\) Б — \(4,\) В — \(2,\) Г — \(3,\) Е — \(4,\) Ж — \(2,\) И — \(6,\) К — \(2.\) Самая большая степень у вершины И. С другой стороны, из таблицы мы определяем, что у \(7\) вершины степень всего лишь \(5.\) Значит, вершина \(7\) — это И и для неё пропущена одна дорога. По графу замечаем, что вершина И не связана только с вершиной В. С остальными вершинами И имеет связь, причём вершин со степенями \(2,\) \(3\) и \(4\) ровно по две. Из таблицы тогда определяем, что вершина \(6\) — это В, а пропущена дорога из вершины \(4\) в вершину \(7.\)
Ответ: \(47\)