Задание 27. Информатика. ЕГЭ. Поляков-7738
- Просмотры: 56
- Изменено: 24 ноября 2024
(А. Кабанов) Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на \(N\) непересекающихся непустых подмножеств (кластеров), таких что точки каждого подмножества лежат внутри сектора круга радиусом \(R\) и центральным углом \(H\) градусов, причём эти сектора между собой не пересекаются. Гарантируется, что такое разбиение существует и единственно. Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра. Расстояние между двумя точками \(A (x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле:
$$
d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}
$$
Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах трёх кластеров с параметрами \(R=5\) и \(H=30.\)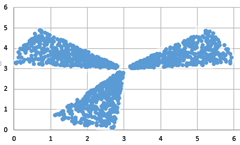 
В каждой строке записана информация о расположении на карте одной звезды: сначала координата x, затем координата y (в условных единицах). Известно, что количество звёзд не превышает \(1000.\) В файле Б такой же структуры хранятся данные о звёздах пяти кластеров с параметрами \(R=10\) и \(H=45.\) Известно, что количество звёзд не превышает \(10~000.\) Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000,\) затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Решение:
Точечная диаграмма, построенная для файла А в табличном процессоре, имеет вид
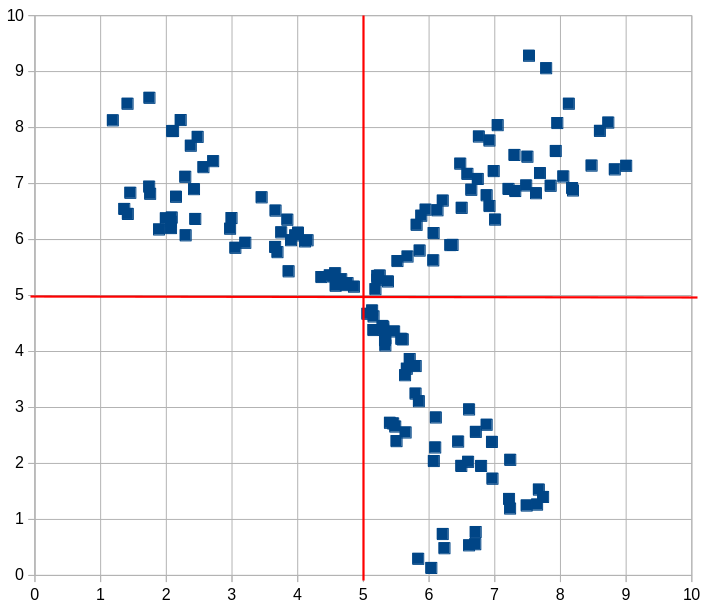
Если ввести систему координат с центром в точке \((5, \, 5)\), то кластеры окажутся в первой, второй и четвёртой координатных четвертях. Это обстоятельство можно использовать для разделения на кластеры.
Точечная диаграмма для файла Б, построенная в табличном процессоре, имеет вид
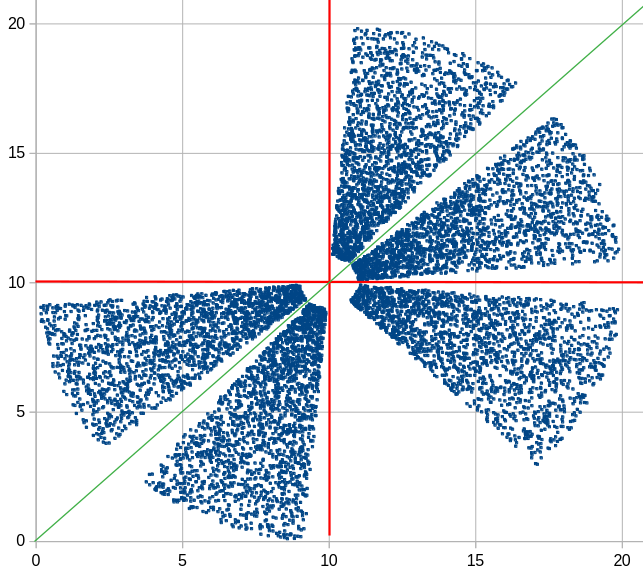
Систему координат удобно ввести так, чтобы начало координат оказалось в точке \((10, \, 10)\). Тогда разделения на кластеры дают координатные оси, а также биссектриса первой и третей координатных четвертей.
Python
from math import dist
def which_cluster(point, task):
x, y = p
if task == 1:
if y - 5 < 0:
return 0
elif x - 5 < 0:
return 1
return 2
elif task == 2:
if x - 10 > 0:
if y - 10 < 0:
return 0
elif (y - 10) / (x - 10) < 1:
return 1
return 2
else:
if (y - 10) / (x - 10) < 1:
return 3
return 4
def get_centroids(clusters):
centroids = []
for cl in clusters:
dmin = 10**10000
for p in cl:
d = sum(dist(p, pt) for pt in cl)
if d < dmin:
dmin = d
c = p
centroids.append(c)
px = 100_000 * sum(p[0] for p in centroids) / len(centroids)
py = 100_000 * sum(p[1] for p in centroids) / len(centroids)
return int(px), int(py)
base = ''
files = ['27a.txt', '27b.txt']
nums_cls = [3, 5]
for task in (1, 2):
clusters = [[], [], [], [], []]
n_cl = nums_cls[task-1]
for line in open(base + files[task-1]):
p = [float(d) for d in line.replace(',', '.').split()]
clusters[which_cluster(p, task)].append(p)
#print([len(t) for t in clusters])
print(*get_centroids(clusters[:n_cl]))
Ответ:
\(532496 \,\, 533164\)
\(1091104 \,\, 954833\)