Задание 27. Информатика. ЕГЭ. Шастин. 18.12.2024
- Просмотры: 206
- Изменено: 1 февраля 2025
(Л. Шастин, В. Лашин) В администрации резиденции Деда Мороза проводится активное обсуждение вопроса эффективности перевозки мириад подарков в канун волшебного Нового Года. Снегурочка настаивает на немедленном внедрении передовых технологий: «Старый мешок с письмами никуда не годится — в этой куче адресов невозможно разобраться, да и Дед уже не тот, даже таблетки не помогают. Если мы срочно не решим эту проблему, наш дорогой Дед Мороз скоро превратится в Санта Клауса! Министерство культуры РФ такое точно не одобрит». В сказочной резиденции с женщинами спорить не принято, тем более с такими молодыми и горячими, как прелестная Снегурочка. Да и аргументы в этот раз звучат убедительно...
Отдел аналитики данных возложил решение обозначенной ранее проблемы на могучие плечи СнегПрогов (снеговиков-программистов). СнегПроги предложили простую концепцию: разделить письма на группы (города) по характеристике места жительства (геопозиции) их отправителей. Благодаря этому гениальному подходу Деду Морозу не придется по сто раз перемещаться между Москвой и Владивостоком, ведь он сможет переходить к доставке подарков по Москве только после того, как развезет все подарки владивостокцам. И Декабрь, Январь и Февраль точно останутся благодарны своему хозяину. К тому же получится сэкономить на бензине, что в наше время совсем не дурно!
Одним городом СнегПроги решили считать такую группу геопозиций (точек, определенных по двум координатам \(x\) и \(y\)), в которой любая из геопозиций удалена от геопозиции из другой группы хотя бы на \(E = 20\) у.е. (условных единиц). А метрикой расстояния между двумя точками (геопозициями) уже традиционно стала формула Евклида: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.$$
Помогите СнегПрогам найти оптимальные геопозиции 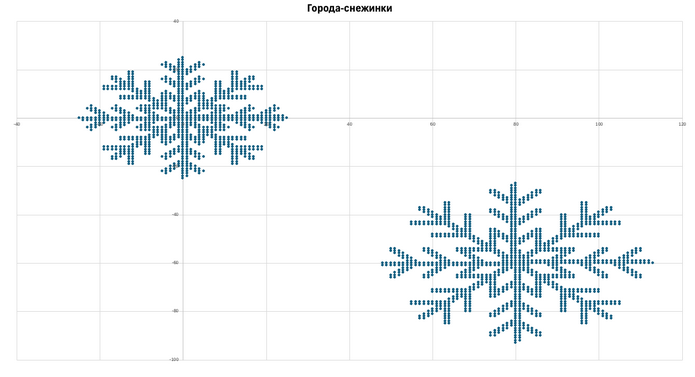 в каждом городе для открытия в них новых филиалов резиденции. Лучшим местом будет считаться такая геопозиция, суммарное расстояние от которой до всех других геопозиций в этом же городе минимально. Если у вас все получится, СнегПроги получат в подарок от Деда Мороза новые чудо-компьютеры, сделанные из льдинок высочайшего качества. А вам в таком случае полагается хорошее настроение =)
в каждом городе для открытия в них новых филиалов резиденции. Лучшим местом будет считаться такая геопозиция, суммарное расстояние от которой до всех других геопозиций в этом же городе минимально. Если у вас все получится, СнегПроги получат в подарок от Деда Мороза новые чудо-компьютеры, сделанные из льдинок высочайшего качества. А вам в таком случае полагается хорошее настроение =)
В файле А хранятся записи об адресах первой партии полученных писем, образующих 2 города. В каждой строке записана информация о двух показателях геопозиции конкретного письма: сначала координата \(x,\) затем координата \(y.\) Известно, что количество записей не превышает \(2200.\) В файле Б хранятся записи об адресах второй партии полученных писем, образующих \(3\) города. Известно, что количество записей не превышает \(15~500.\) Структура хранения информации в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты новых филиалов резиденции для всех городов, а затем вычислите два числа: \(S_x\) — среднее арифметическое абсцисс этих филиалов, и \(S_y\) — среднее арифметическое их ординат. В ответе запишите четыре числа: в первой строке сначала целую часть значения \(S_x,\) затем целую часть значения \(S_y\) для файла А, во второй строке — аналогичные данные для файла Б.
Решение:
Python
from math import dist
from turtle import *
def visualize(clusters):
tracer(0)
screensize(2500, 2500)
up()
k = 1
colors = ('red', 'green', 'blue')
for cl, c in zip(clusters, colors):
for p in cl:
x, y = p
goto(x * k, y * k)
dot(3, c)
ht()
update()
base = ''
files = ['27_A.txt', '27_B.txt']
for task in (1, 2):
data = [tuple(map(int, line.split())) for line in open(base + files[task-1])]
clusters = []
while data:
clusters.append([data.pop()])
for pt in clusters[-1]:
neigh = [p for p in data if dist(p, pt) < 20]
clusters[-1] += neigh
for p in neigh:
data.remove(p)
#print(len(clusters))
#if task == 2: visualize(clusters)
centers = []
for cl in clusters:
dmin = 10**1000
for p in cl:
d = sum(dist(p, pt) for pt in cl)
if d < dmin:
dmin = d
c = p
centers.append(c)
px = int(sum(p[0] for p in centers) / len(centers))
py = int(sum(p[1] for p in centers) / len(centers))
print(px, py)
Ответ:
\(40\) \(-30\)
\(-19\) \(-176\)
Визуализация кластеров с помощью графики модуля Turtle
Файл A

Файл B