Задание 27. Информатика. ЕГЭ. Шастин. 30.11.2024
- Просмотры: 525
- Изменено: 1 февраля 2025
(Л. Шастин) Ведущие специалисты отдела бизнес-аналитики торгового маркетплейса «Ozonyol» собирают статистику и изучают предпочтения покупателей за период летних и осенних продаж. Перед ними стоит задача — проанализировать рынок и сделать выводы об уровне спроса на товары различных категорий для выделения наиболее перспективных траекторий развития площадки с привлечением инвестиционных средств. По итогам сбора информации имеется набор данных, включающих записи о товарах, каждый из которых содержит три показателя — номер сегмента товара, характеризующий его расположение на сайте, коэффициент успешных конверсий и уровень заинтересованности поуапателей, выраженный в коэффициенте их активности. Общий спрос на товар вычисляется как среднее арифметическое второго и третьего показателей. На основании полученной информации строится графический отчёт, отражающий общий спрос на товар в зависимости от его номера сегмента, в котором записи, лежащие в области окружности с радиусом \(R\), выделяются в отдельные кластеры. В итоге решено привлекать средства на продвижение товаров только из кластеров, содержащих хотя бы \(K\) записей, причем первые вложения направить в товары-медоиды. Медоидом (центром) кластера называется такая запись о товаре, суммарное расстояние от которой до других записей в кластере минимально. Метрикой расстояния между двумя записями \(A(x_1, \, x_2)\) и \(B(x_2, \, y_2)\) является формула Евклида: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.$$ Примечание. Гарантируется, что товар принадлежит только одному из кластеров.
В файле A в первой строке записаны числа \(R\) и \(K.\) В остальных строках хранятся записи о товарах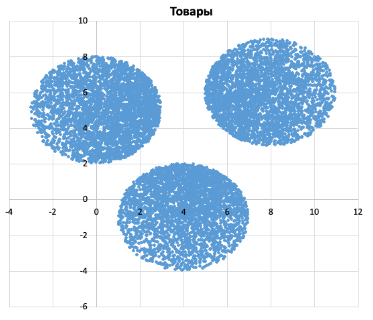 
за период летних продаж, образующих \(3\) кластера. В каждой строке записана информация о трёх показателях конкретного товара: сначала номер сегмента, затем коэффициент успешных конверсий и коэффициент активности. Известно, что количество записей не превышает \(1100.\) В файле Б хранятся записи о товарах за период осенних продаж, образующих \(6\) кластеров, и соответствующие осенним продажам числа \(R\) и \(K.\) Известно, что количество записей не превышает \(11~000.\) Структура хранения информации о товарах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты медоидов (центров) всех кластеров, для продвижения которых будут привлечены инвестиционные средства, а затем вычислите два числа: \(S_x\) — среднее арифметическое абсцисс центров кластеров, и \(S_y\) — среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(S_x \times 100~000,\) затем целую часть произведения \(S_y \times 100~000\) для файла А, во второй строке — аналогичные данные для файла Б.
Решение:
Решение методом DBSCAN. Подбором установлено, что \(\varepsilon\) для файла А равен \(1,\) а для файла Б — \(0{,}2.\) Для контроля выводится еще дополнительная информация.
Python
from math import dist
base = ''
files = ['27_A.txt', '27_B.txt']
for task in (1, 2):
fd = open(base + files[task-1])
R, K = map(float, fd.readline().split())
print('R=', R, 'K=', K)
data = []
for line in fd:
s, k1, k2 = map(float, line.replace(',', '.').split())
data.append([s, (k1 + k2) / 2])
clusters = []
while data:
eps = [1, 0.2]
clusters.append([data.pop(0)])
for point in clusters[-1]:
neigh = [p for p in data if dist(point, p) < eps[task-1]]
clusters[-1] += neigh
for p in neigh:
data.remove(p)
print('Получилось всего кластеров', len(clusters))
print('Количество товаров в кластерах',[len(c) for c in clusters])
clusters = [cl for cl in clusters if len(cl) >= K]
print('Убрали маленькие кластеры')
print('Всего осталось', len(clusters))
print('Количество товаров в кластерах', [len(c) for c in clusters])
medoids = []
for cl in clusters:
dmin = 10**10000
for point in cl:
d = sum(dist(point, p) for p in cl)
if d < dmin:
dmin = d
c = point
medoids.append(c)
px = 100_000 * sum(p[0] for p in medoids) / len(medoids)
py = 100_000 * sum(p[1] for p in medoids) / len(medoids)
print('px = ', int(px), 'py =', int(py))
Ответ:
\(728724 \,\, 506096\)
\(328813 \,\, 419784\)