Задание 27. Информатика. ЕГЭ. Статград. 24.10.2024-1
- Просмотры: 781
- Изменено: 1 февраля 2025
В лаборатории проводится эксперимент, состоящий из множества испытаний. Результат каждого испытания представляется в виде пары чисел. Для визуализации результатов эта пара рассматривается как координаты точки на плоскости, и на чертеже отмечаются точки, соответствующие всем испытаниям.
По результатам эксперимента проводится кластеризация полученных результатов: на плоскости выделяется несколько кластеров – прямоугольников размером \(3 \times 3\) так, что каждая точка попадает ровно в один кластер.
Центроидом кластера называется та из входящих в него точек, для которой минимальна сумма расстояний до всех остальных точек кластера. Обработка результатов эксперимента включает следующие шаги:
- кластер, содержащий наименьшее число точек, исключается;
- определяются центроиды всех оставшихся кластеров;
- для найденных центроидов вычисляется средняя точка. Средней для группы точек называется точка (не обязательно входящая в группу), координаты которой определяются как средние арифметические значения координат всех точек группы.
В файле записан протокол проведения эксперимента. Каждая строка файла содержит два числа: координаты \(X\) и \(Y\) точки, соответствующей одному испытанию. По данному протоколу надо определить среднюю точку центроидов всех кластеров за исключением содержащего наименьшее число точек.
Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. По данным каждого из представленных файлов определите координаты средней точки по описанным выше правилам. В ответе запишите четыре числа: сначала (в первой строке) координаты \(X\) и \(Y\) средней точки для файла A, затем (во второй строке) координаты \(X\) и \(Y\) средней точки для файла B. В качестве значения координаты указывайте целую часть от умножения числового значения координаты на \(10~000.\)
Решение:
Точечная диаграмма, построенная для файла А в табличном процессоре, имеет вид
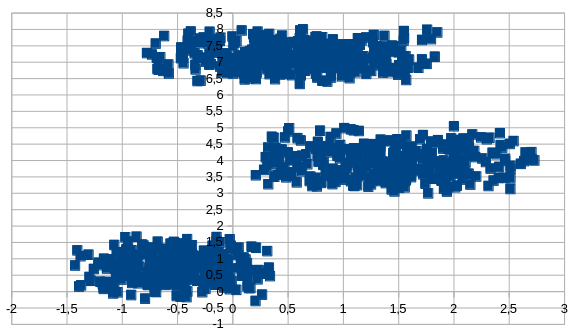
Видно, что кластеры можно разделить, прямой \(y = 2.5\) и \(y = 5.5\).
Точечная диаграмма для файла Б, построенная в табличном процессоре, имеет вид

Левые кластеры отделяется от остальных прямой \(x = 3\). Сами эти кластеры разделяются прямой \(y = 2\). Правые кластеры отделяются друг от друга прямыми \(y =1.25\), \(y =4.75\).
Python
def which_cluster(point, task):
x, y = point
if task == 1:
if y < 2.5:
return 0
elif y < 5.5:
return 1
else:
return 2
if task == 2:
if x < 3:
if y < 2:
return 0
else:
return 1
else:
if y < 1.25:
return 2
elif y < 4.75:
return 3
return 4
def dist(p1, p2):
x1, y1 = p1
x2, y2 = p2
return ((x1 - x2)**2 + (y1 - y2)**2)**0.5
base = ''
files = ['27A.txt', '27B.txt']
for t in (1, 2):
clusters = [[], [], [], [], []]
for line in open(base + files[t-1]):
point = [float(i) for i in line.split()]
clusters[which_cluster(point, t)].append(point)
len_cl = {len(c): i for i, c in enumerate(clusters) if c != []}
work_clusters = [v for k, v in len_cl.items() if k != min(len_cl.keys())]
centroids = []
for cl in work_clusters:
dmin = 10**100
for p in clusters[cl]:
d = sum(dist(p, pt) for pt in clusters[cl])
if d < dmin:
dmin = d
c = p
centroids.append(c)
mx, my = 0, 0
for p in centroids:
mx += p[0]
my += p[1]
print(int(mx * 10000 / len(centroids)), int(my * 10000 /len(centroids)))
Ответ:
\(9877 \,\, 55816\)
\(26104 \,\, 34664\)