Задание 4. Информатика. ЕГЭ. Поляков-7404
- Просмотры: 3405
- Изменено: 1 февраля 2025
(Е. Джобс) По каналу связи передаются сообщения, содержащие только буквы из набора Е, Г, Э, Б, Л, И, З, К, О. Передаваемое сообщение переводится в двоичный код. При выбранном методе кодирования ни одно кодовое слово не может являться началом другого кодового слова. Такой код обеспечивает однозначное декодирование переданного сообщения. Для нескольких букв кодовые слова известны: Е – \(01\), Э – \(1010\), З – \(1100\), К – \(0010\). Какое минимальное количество двоичных знаков потребуется для кодирования слова БИБЛИОЛОГ?
Решение:
В слове БИБЛИОЛОГ по две буквы Б, И, Л, О и одна Г. Двойные буквы стараемся разместить как можно выше в бинарном дереве.
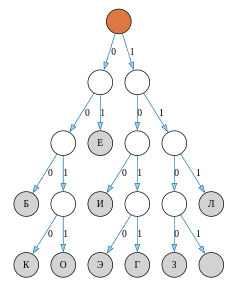
Одна из возможных кодировок: Б — \(000\), И — \(100\), Л — \(111\), О — \(0011\), Г — \(1011\). Итого \(6 \cdot 3 + 3 \cdot 4 = 30\) двоичных знаков.
Ответ: \(30\)