Задание 4. Информатика. ЕГЭ. Шастин. 30.11.2024
- Просмотры: 1376
- Изменено: 1 февраля 2025
(Л. Шастин) По каналу связи передаются сообщения, содержащие только восемь букв: А, Б, В, Г, Д, Е, Ж и З. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны:
| А | \(000\) |
| Б | \(001\) |
| В | \(0101\) |
| Г | \(0100\) |
| Д | \(011\) |
Какое наименьшее количество двоичных знаков потребуется для кодирования трёх оставшихся букв? В ответе запишите произведение длин кодовых слов для букв: Е, Ж, З.
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Решение:
Один из вариантов кодирования указанных трёх букв указан на графе ниже.
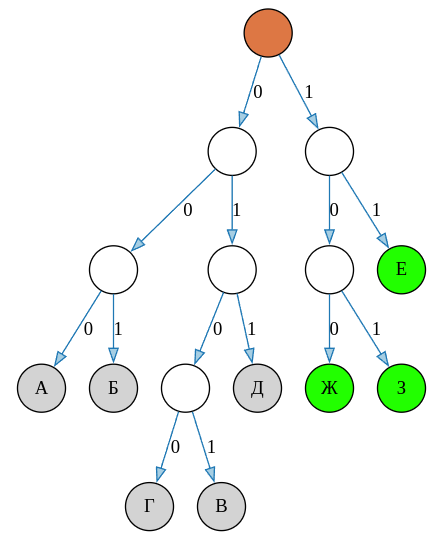
Буква Е кодируется двумя символами, а Ж и З — тремя. Поэтому произведение длин кодовых слов этих букв равно \(2 \cdot 3 \cdot 3 = 18.\)
Ответ: \(18\)